题目内容
已知函数 为偶函数,且函数y=f(x)图象的两相邻对称轴的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴的距离为 .
.(1)求f(x)的解析式;
(2)将函数y=f(x)的图象向右平移
 个单位后,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,得到函数y=g(x)的图象,求g(x)的单调递减区间.(3)若存在
 ,使不等式f(x)<m成立,求实数m的取值范围.
,使不等式f(x)<m成立,求实数m的取值范围.
【答案】分析:(1)化简f(x)的解析式,利用f(x)为偶函数求出ϕ值,再利用周期等于π,求出ω,即得f(x)的解析式.
(2) ,由
,由 ,解得x的范围,即得函数的单调递减区间.
,解得x的范围,即得函数的单调递减区间.
(3)依题可得只需 时,m大于f(x)的最小值即可.
时,m大于f(x)的最小值即可.
解答:解:(1)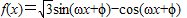 =
=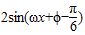 ,
,
∵f(x)为偶函数,所以 ,又0<ϕ<π,所以
,又0<ϕ<π,所以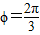 ,
,
函数y=f(x)图象的两相邻对称轴的距离为 ,所以周期T=π,于是ω=2,所以,
,所以周期T=π,于是ω=2,所以,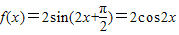 .
.
(2)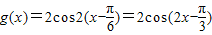 ,由
,由 ,
,
解得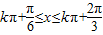 ,所以函数的单调递减区间为
,所以函数的单调递减区间为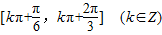 .
.
(3)依题可得只需 时,m>(f(x))min =-2.
时,m>(f(x))min =-2.
点评:本题考查y=Asin(ωx+∅)的图象的变换,正弦函数的奇偶性、单调性及最值,求g(x)的单调递减区间是解题的难点.
(2)
 ,由
,由 ,解得x的范围,即得函数的单调递减区间.
,解得x的范围,即得函数的单调递减区间.(3)依题可得只需
 时,m大于f(x)的最小值即可.
时,m大于f(x)的最小值即可.解答:解:(1)
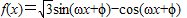 =
=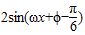 ,
,∵f(x)为偶函数,所以
 ,又0<ϕ<π,所以
,又0<ϕ<π,所以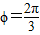 ,
,函数y=f(x)图象的两相邻对称轴的距离为
 ,所以周期T=π,于是ω=2,所以,
,所以周期T=π,于是ω=2,所以,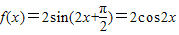 .
.(2)
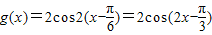 ,由
,由 ,
,解得
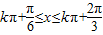 ,所以函数的单调递减区间为
,所以函数的单调递减区间为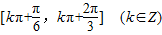 .
.(3)依题可得只需
 时,m>(f(x))min =-2.
时,m>(f(x))min =-2.点评:本题考查y=Asin(ωx+∅)的图象的变换,正弦函数的奇偶性、单调性及最值,求g(x)的单调递减区间是解题的难点.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 的值.
的值. 的值。
的值。 为偶函数,且
为偶函数,且 在
在 上递减,设
上递减,设 ,
, ,
, ,则
,则 的大小关系正确的是( )
的大小关系正确的是( ) (B)
(B) (C)
(C) (D)
(D)
 为偶函数,且在
为偶函数,且在 上为增函数.
上为增函数. 的值,并确定
的值,并确定 的解析式;
的解析式; 且
且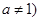 ,是否存在实数
,是否存在实数 使
使 在区间
在区间 上的最大值为2,若存在,求出
上的最大值为2,若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由. 为偶函数, 且
为偶函数, 且
 的值;
的值; 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的