题目内容
焦点分别为(0,5 )和(0,-5
)和(0,-5 )的椭圆截直线y=3x-2所得椭圆的弦的中点的横坐标为
)的椭圆截直线y=3x-2所得椭圆的弦的中点的横坐标为 ,求此椭圆方程.
,求此椭圆方程.
解:由题意可设椭圆方程为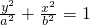 (a>b>0),
(a>b>0),
∵c=5
∴a2-b2=50①
把直线方程y=3x-2代入椭圆方程整理得(a2+9b2)x2-12b2x+b2(4-a2)=0.
设弦的两个端点为A(x1,y1),B(x2,y2),则由根与系数的关系可得,
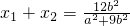
由中点坐标公式可得,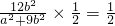
∴a2=3b2②
联立①②可得,a2=75,b2=25
∴椭圆方程为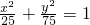
分析:根据焦点坐标得出a2-b2=50,将直线的方程与椭圆的方程组成方程组,消去y得到关于x的方程,再根据根与系数的关系求得AB的中点的横坐标的表达式,最后根据联立的方程求出其a,b即可求椭圆的方程.
点评:本题主要考查了椭圆的标准方程、直线与圆锥曲线的综合问题.直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置关系的判定,弦长问题、最值问题、对称问题、轨迹问题等.注意本题还金额以考虑利用点差法进行求解
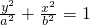 (a>b>0),
(a>b>0),∵c=5

∴a2-b2=50①
把直线方程y=3x-2代入椭圆方程整理得(a2+9b2)x2-12b2x+b2(4-a2)=0.
设弦的两个端点为A(x1,y1),B(x2,y2),则由根与系数的关系可得,
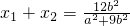
由中点坐标公式可得,
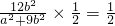
∴a2=3b2②
联立①②可得,a2=75,b2=25
∴椭圆方程为
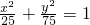
分析:根据焦点坐标得出a2-b2=50,将直线的方程与椭圆的方程组成方程组,消去y得到关于x的方程,再根据根与系数的关系求得AB的中点的横坐标的表达式,最后根据联立的方程求出其a,b即可求椭圆的方程.
点评:本题主要考查了椭圆的标准方程、直线与圆锥曲线的综合问题.直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置关系的判定,弦长问题、最值问题、对称问题、轨迹问题等.注意本题还金额以考虑利用点差法进行求解

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
 )和(0,﹣5
)和(0,﹣5 )的椭圆截直线y=3x﹣2所得椭圆的弦的中点的横坐标为
)的椭圆截直线y=3x﹣2所得椭圆的弦的中点的横坐标为 ,求此椭圆方程.
,求此椭圆方程. )和(0,-5
)和(0,-5 )的椭圆截直线y=3x-2所得椭圆的弦的中点的横坐标为
)的椭圆截直线y=3x-2所得椭圆的弦的中点的横坐标为 ,求此椭圆方程.
,求此椭圆方程.