题目内容
α-l-β是直二面角,直线a与α所成角为30°,则a与β所成角( )A.60°
B.小于60°
C.取值范围为[0°,90°]
D.取值范围为[0°,60°]
【答案】分析:设线段AB夹在直二面角α-l-β内,A∈α,B∈β,如果AB与平面α、β所成的角分别为α和β,过A在α内做AC垂直于l于C点,过B在β内做BD垂直于l于D点. 在β内做BE平行l,在β内做CE平行BD,交点为E,连接AE,AD,BC,根据AD>AC判断∠ABC<∠ABD,由于∠ABD+∠DAB=90°进而知α+β<90°,当AB与l垂直时α+β=90° 当AB与l平行时α+β=0,最后综合答案可得α+β的范围为0≤α+β≤90°;再结合直线a与α所成角为30°即可得到答案.
解答:解:设线段AB夹在直二面角α-l-β内,A∈α,B∈β,
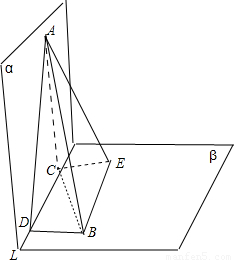
如果AB与平面α、β所成的角分别为α和β,
过A在α内做AC垂直于l于C点,过B在β内做BD垂直于l于D点.
在β内做BE平行l,在β内做CE平行BD,交点为E,连接AE,AD,BC
则∠DAB=α,∠ABC=β,sin∠ABC=ACAB,sin∠DAB=ADAB
因为AD>AC,所以∠ABC<∠ABD,
∠ABD+∠DAB=90°,所以α+β<90°
当AB与l垂直时α+β=90°
当AB与l平行时α+β=0
∴0≤α+β≤90°;
又因为直线a与α所成角为30°;
所以:a与β所成角的范围是:[0,,60°]
故选:D.
点评:本题主要考查了空间中直线与平面的位置关系.解题的关键是判断出当直线与两面角的棱平行或垂直时的情况.
解答:解:设线段AB夹在直二面角α-l-β内,A∈α,B∈β,

如果AB与平面α、β所成的角分别为α和β,
过A在α内做AC垂直于l于C点,过B在β内做BD垂直于l于D点.
在β内做BE平行l,在β内做CE平行BD,交点为E,连接AE,AD,BC
则∠DAB=α,∠ABC=β,sin∠ABC=ACAB,sin∠DAB=ADAB
因为AD>AC,所以∠ABC<∠ABD,
∠ABD+∠DAB=90°,所以α+β<90°
当AB与l垂直时α+β=90°
当AB与l平行时α+β=0
∴0≤α+β≤90°;
又因为直线a与α所成角为30°;
所以:a与β所成角的范围是:[0,,60°]
故选:D.
点评:本题主要考查了空间中直线与平面的位置关系.解题的关键是判断出当直线与两面角的棱平行或垂直时的情况.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
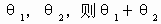 的取值区间为________.
的取值区间为________.