题目内容
设向量
(1)若 ,求
,求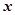 的值
的值
(2)设函数 ,求
,求 的取值范围
的取值范围
(1) ;(2)
;(2) .
.
解析试题分析: (1)利用向量的模长公式 化简得到关于
化简得到关于 关系式,进而求得
关系式,进而求得 的值,再利用三角函数值,结合角的范围求得
的值,再利用三角函数值,结合角的范围求得 的值;(2)利用三角恒等变形化成
的值;(2)利用三角恒等变形化成 ,再利用三角函数的图像与性质求解.规律总结:1.涉及平面向量的模长、数量积等运算时,要合理选用公式(向量形式或坐标形式); 2.三角恒等变形的关键,要正确运用公式及其变形,如:二倍角公式的变形
,再利用三角函数的图像与性质求解.规律总结:1.涉及平面向量的模长、数量积等运算时,要合理选用公式(向量形式或坐标形式); 2.三角恒等变形的关键,要正确运用公式及其变形,如:二倍角公式的变形 ,
,
求 在某区间的值域时,一定要结合正弦函数、余弦函数的图像求解.
在某区间的值域时,一定要结合正弦函数、余弦函数的图像求解.
注意点:学生对公式及其变形运用的灵活性不够,学生应加强公式的记忆和应用;求 的值域时,学生不善于利用数形结合思想,往往想当然,最大值为1,最小值为-1.
的值域时,学生不善于利用数形结合思想,往往想当然,最大值为1,最小值为-1.
试题解析:(1)



= 又
又 ;
; 的取值范围是
的取值范围是 .
.
考点:1.平面向量的数量积,2.三角恒等变形,3.三角函数的图像与性质

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 满足
满足 ,则
,则
 ,
, .
. ,求
,求 ;
; 与
与 垂直,求当
垂直,求当 为何值时,
为何值时, .
. 为坐标原点,
为坐标原点, =(
=( ),
), =(1,
=(1, ),
),  .
. 的定义域为[-
的定义域为[- ,
, ],求y=
],求y= 的定义域为[
的定义域为[ 的值.
的值. 满足|
满足| |=|
|=| |=1,且|2
|=1,且|2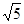 .
. 的值;
的值;  与
与 夹角
夹角 .
. ,
, , 且
, 且
 的解析式;
的解析式; 时,
时,  的值.
的值. :
: 的焦点为
的焦点为 ,若过点
,若过点 的直线与抛物线相交于
的直线与抛物线相交于 两点,且
两点,且 .
. 为抛物线
为抛物线 ,
, 为
为 的最小值.
的最小值. +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为
,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为 .
.
 的直线l,与椭圆交于E,F点,试判断∠EF2F是锐角、直角还是钝角,并写出理由;
的直线l,与椭圆交于E,F点,试判断∠EF2F是锐角、直角还是钝角,并写出理由; 轴于点N,M,若直线OT与过点M,N 的圆G相切,切点为T.证明:线段OT的长为定值,并求出该定值.
轴于点N,M,若直线OT与过点M,N 的圆G相切,切点为T.证明:线段OT的长为定值,并求出该定值. ,则向量b与
,则向量b与 的夹角是 。
的夹角是 。