题目内容
下列命题错误的是
| A.命题“若m > 0,则方程x2+x-m=0有实数根”的逆否命题为:“若方程x2+x-m=0无实数根,则m≤0”. |
| B.“x=1”是“x2-3x + 2=0”的充分不必要条件. |
C.若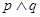 为假命题,则p ,q均为假命题. 为假命题,则p ,q均为假命题. |
D.对于命题p: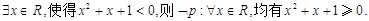 |
C
试题分析:四种命题的关系,主要是对于逆否命题的运用,同时利用集合的思想,能判定命题间的包含关系,从而得到充分条件的判定。
由于选项A中,若m > 0,则方程x2+x-m=0有实数根”的逆否命题为,将原命题的条件的否定作为其逆否命题的结论,将原命题中结论的否定作为其逆否命题的条件,可知为若方程x2+x-m=0无实数根,则m≤0”,因此正确。
选项B中, 命题的结论“x2-3x + 2=0”等价于x=1,或x=2,而命题的条件是x=1,可知条件表示的集合小,则利用小集合是大集合成立的充分不必要条件,故正确。
选项C,中,且命题为假命题,则说明至少有一个假命题,因此错误。
选项D中,对于特称命题的否定,就是将存在改为任意,结论变为否定即可。故正确,因此答案为C.
点评:简易逻辑的考查主要是侧重于命题的真值,以及四种命题的关系,以及充分条件的判定的考查上,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
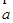 ∥
∥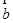
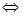 存在唯一的实数
存在唯一的实数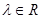 ,使得
,使得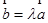 ;
;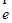 为单位向量,且
为单位向量,且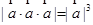 ;
;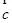 共线,则
共线,则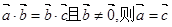
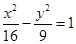 与椭圆
与椭圆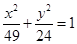 有相同的焦点;
有相同的焦点;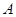 、
、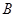 为两个定点,
为两个定点,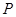 为动点,且
为动点,且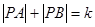 ,其中常数
,其中常数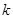 为正实数,则动点
为正实数,则动点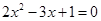 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;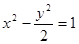 的右焦点
的右焦点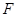 作直线
作直线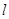 交双曲线于
交双曲线于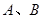 两点,若
两点,若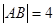 ,则这样的直线
,则这样的直线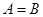 ,则
,则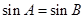 ”的逆否命题是( )
”的逆否命题是( ) ,则
,则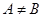
 ,其中
,其中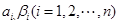 均为常数,下列说法正确的有
均为常数,下列说法正确的有 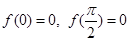 ,则对于任意
,则对于任意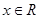 ,
,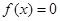 恒成立;
恒成立;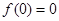 ,则
,则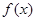 是奇函数; (3) 若
是奇函数; (3) 若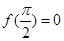 ,则
,则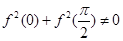 ,且当
,且当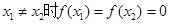 ,则
,则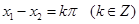 ;
;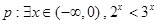 ,命题
,命题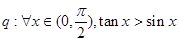 ,则下列命题为真命题的是
,则下列命题为真命题的是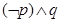
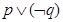
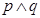
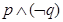
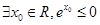
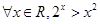
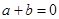 的充要条件是
的充要条件是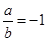
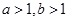 是
是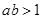 的充分条件
的充分条件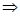 a∈A∪B ②A
a∈A∪B ②A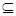 B
B