题目内容
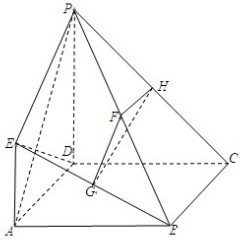 (2013•朝阳区二模)如图,四边形ABCD是正方形,EA⊥平面ABCD,EA∥PD,AD=PD=2EA=2,F,G,H分别为PB,EB,PC的中点.
(2013•朝阳区二模)如图,四边形ABCD是正方形,EA⊥平面ABCD,EA∥PD,AD=PD=2EA=2,F,G,H分别为PB,EB,PC的中点.(Ⅰ)求证:FG∥平面PED;
(Ⅱ)求平面FGH与平面PBC所成锐二面角的大小;
(Ⅲ)在线段PC上是否存在一点M,使直线FM与直线PA所成的角为60°?若存在,求出线段PM的长;若不存在,请说明理由.
分析:(Ⅰ)由三角形的中位线定理得到线线平行,然后直接利用线面平行的判定定理得到线面平行;
(Ⅱ)建立空间直角坐标系,根据两个平面的法向量所成的角与二面角相等或互补,由两个平面法向量所成的角求解二面角的大小;
(Ⅲ)假设存在点M,由共线向量基本定理得到M点的坐标,其中含有一个未知量,然后利用直线FM与直线PA所成的角为
60°转化为两向量所成的角为60°,由两向量的夹角公式求出M点的坐标,得到的M点的坐标符合题意,说明假设成立,最后得到结论.
(Ⅱ)建立空间直角坐标系,根据两个平面的法向量所成的角与二面角相等或互补,由两个平面法向量所成的角求解二面角的大小;
(Ⅲ)假设存在点M,由共线向量基本定理得到M点的坐标,其中含有一个未知量,然后利用直线FM与直线PA所成的角为
60°转化为两向量所成的角为60°,由两向量的夹角公式求出M点的坐标,得到的M点的坐标符合题意,说明假设成立,最后得到结论.
解答:(Ⅰ)证明:因为F,G分别为PB,BE的中点,所以FG∥PE.
又FG?平面PED,PE?平面PED,所以FG∥平面PED.
(Ⅱ)解:因为EA⊥平面ABCD,所以PD⊥平面ABCD,所以PD⊥AD,PD⊥CD.
又因为四边形ABCD是正方形,所以AD⊥CD.
如图建立空间直角坐标系,
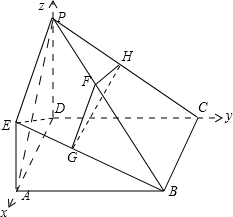
因为AD=PD=2EA,所以D(0,0,0),P(0,0,2),A(2,0,0),
C(0,2,0),B(2,2,0),E(2,0,1).
因为F,G,H分别为PB,EB,PC的中点,所以F(1,1,1),G(2,1,
),H(0,1,1).
所以
=(-1,0,
),
=(-2,0,
),
设
=(x1,y1,z1)为平面FGH的一个法向量,则
,即
,
再令y1=1,得
=(0,1,0).
=(2,2,-2),
=(0,2,-2),
设
=(x2,y2,z2)为平面PBC的一个法向量,则
,即
,
令z2=1,得
=(0,1,1).
所以|cos<
,
>|=
=
=
.
所以平面FGH与平面PBC所成锐二面角的大小为
.
(Ⅲ)在线段PC上存在点M,使直线FM与直线PC所成角为60°
证明:假设在线段PC上存在点M,使直线FM与直线PC所成角为60°.
依题意可设
=λ
,其中0≤λ≤1.
由
=(0,2,-2),则
=(0,2λ,-2λ).
又因为
=
+
,
=(-1,-1,1),
所以
=(-1,2λ-1,1-2λ).
又直线FM与直线PA成60°角,
(2,0,-2),
所以|cos<
,
>|=
,即
=
,解得:λ=
.
所以
=(0,
,-
),|
|=
=
.
所以,在线段PC上存在点M,使直线FM与直线PC所成角为60°,此时PM的长为
.
又FG?平面PED,PE?平面PED,所以FG∥平面PED.
(Ⅱ)解:因为EA⊥平面ABCD,所以PD⊥平面ABCD,所以PD⊥AD,PD⊥CD.
又因为四边形ABCD是正方形,所以AD⊥CD.
如图建立空间直角坐标系,

因为AD=PD=2EA,所以D(0,0,0),P(0,0,2),A(2,0,0),
C(0,2,0),B(2,2,0),E(2,0,1).
因为F,G,H分别为PB,EB,PC的中点,所以F(1,1,1),G(2,1,
| 1 |
| 2 |
所以
| GF |
| 1 |
| 2 |
| GH |
| 1 |
| 2 |
设
| n1 |
|
|
再令y1=1,得
| n1 |
| PB |
| PC |
设
| n2 |
|
|
令z2=1,得
| n2 |
所以|cos<
| n1 |
| n2 |
|
| ||||
|
|
| |(0,1,0)•(0,1,1)| | ||
1×
|
| ||
| 2 |
所以平面FGH与平面PBC所成锐二面角的大小为
| π |
| 4 |
(Ⅲ)在线段PC上存在点M,使直线FM与直线PC所成角为60°
证明:假设在线段PC上存在点M,使直线FM与直线PC所成角为60°.
依题意可设
| PM |
| PC |
由
| PC |
| PM |
又因为
| FM |
| FP |
| PM |
| FP |
所以
| FM |
又直线FM与直线PA成60°角,
| PA |
所以|cos<
| FM |
| PA |
| 1 |
| 2 |
| 1 |
| 2 |
| |-2-2+4λ| | ||||
2
|
| 5 |
| 8 |
所以
| PM |
| 5 |
| 4 |
| 5 |
| 4 |
| PM |
0+2×(
|
5
| ||
| 4 |
所以,在线段PC上存在点M,使直线FM与直线PC所成角为60°,此时PM的长为
5
| ||
| 4 |
点评:本题考查了线面平行的判定,考查了线线角和面面角,训练了利用平面法向量求解二面角的大小,解答此类问题的关键是正确建系,准确求用到的点的坐标,此题是中档题.

练习册系列答案
相关题目
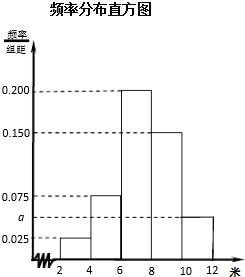 (2013•朝阳区二模)为了解某市今年初二年级男生的身体素质状况,从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试.成绩低于6米为不合格,成绩在6至8米(含6米不含8米)的为及格,成绩在8米至12米(含8米和12米,假定该市初二学生掷实心球均不超过12米)为优秀.把获得的所有数据,分成[2,4),[4,6),[6,8),[8,10),[10,12]五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
(2013•朝阳区二模)为了解某市今年初二年级男生的身体素质状况,从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试.成绩低于6米为不合格,成绩在6至8米(含6米不含8米)的为及格,成绩在8米至12米(含8米和12米,假定该市初二学生掷实心球均不超过12米)为优秀.把获得的所有数据,分成[2,4),[4,6),[6,8),[8,10),[10,12]五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.