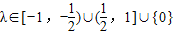题目内容
已知在R上的奇函数f(x),当x∈(0,+∞)时,f(x)=
,下列说法错误的是( )
| 2x |
| 2x+1 |
分析:根据题目给出的奇函数在x∈(0,+∞)时的解析式,求出函数在x=0和x∈(-∞,0)的解析式,即可判断选项B,然后求出f(-1)的值可判断选项A,运用函数单调性得定义可判断选项D,对于选项C,实则是求函数f(x)在R上的值域.
解答:解:因为f(x)是R上的奇函数,所以f(0)=0,
设x∈(-∞,0),则-x∈(0,+∞),则f(x)=-f(-x)=-
=-
.由此判断选项B正确;
而f(-1)=-
=-
,所以选项A正确;
因为当x∈(-∞,0)时,2x∈(0,1),2x+1∈(1,2),-
∈(-1,-
);当x=0时,f(x)=0;当x∈(0,+∞)时,2x>1,0<
<1,
∈(
,1).
所以,若y=f(x)-λ在R上存在零点,则λ∈(-1,-
)∪(
,1)∪{0},选项C中多取了-1和1,所以不正确;
设-1<x1<x2≤0,则f(x1)-f(x2)=-
+
=
,
因为-1<x1<x2≤0,所以2x1-2x2<0,所以f(x1)<f(x2),所以f(x)在(-10,]上是增函数,不是单调递减函数,所以选项D正确;
所以说法错误的只有选项C.
故选C.
设x∈(-∞,0),则-x∈(0,+∞),则f(x)=-f(-x)=-
| 2-x |
| 2-x+1 |
| 1 |
| 2x+1 |
而f(-1)=-
| 1 |
| 2-1+1 |
| 2 |
| 3 |
因为当x∈(-∞,0)时,2x∈(0,1),2x+1∈(1,2),-
| 1 |
| 2x+1 |
| 1 |
| 2 |
| 1 |
| 2x |
| 2x |
| 2x+1 |
| 1 |
| 2 |
所以,若y=f(x)-λ在R上存在零点,则λ∈(-1,-
| 1 |
| 2 |
| 1 |
| 2 |
设-1<x1<x2≤0,则f(x1)-f(x2)=-
| 1 |
| 2x1+1 |
| 1 |
| 2x2+1 |
| 2x1-2x2 |
| (2x1+1)(2x2+1) |
因为-1<x1<x2≤0,所以2x1-2x2<0,所以f(x1)<f(x2),所以f(x)在(-10,]上是增函数,不是单调递减函数,所以选项D正确;
所以说法错误的只有选项C.
故选C.
点评:本题考查了函数的奇偶性的性质,考查了函数值域的求法,考查了函数单调性的定义,解答此题的关键是求出函数在R上的解析式,此题为中档题.

练习册系列答案
相关题目
 ,下列说法错误的是( )
,下列说法错误的是( )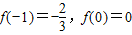
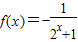

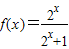 ,下列说法错误的是( )
,下列说法错误的是( )