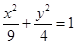题目内容
在坐标平面上,圆C的圆心在原点且半径为2,已知直线L与圆C相交,则直线L与下列图形一定相交的是( )
| A、y=x2 | ||||
B、y=(
| ||||
| C、x2+y2=3 | ||||
D、
|
分析:圆心在原点且半径为2的圆C的方程是x2+y2=4,当直线L过二三四象限时,它不与y=x2相交;当直线L在三四象限平行于x轴时,它不与y=(
)x相交;当直线L到原点的距离大于
小于2时,它不与x2+y2=3相交;
+
=1包含x2+y2=4,直线L一定和椭圆
+
=1相交.
| 1 |
| 2 |
| 3 |
| x2 |
| 9 |
| y2 |
| 4 |
| x2 |
| 9 |
| y2 |
| 4 |
解答:解:圆心在原点且半径为2的圆C的方程是x2+y2=4,
当直线L过二三四象限时,它不与y=x2相交;
当直线L在三四象限平行于x轴时,它不与y=(
)x相交;
当直线L到原点的距离大于
小于2时,它不与x2+y2=3相交;
∵
+
=1包含x2+y2=4,
∴与圆C相交的直线L一定和椭圆
+
=1相交.
当直线L过二三四象限时,它不与y=x2相交;
当直线L在三四象限平行于x轴时,它不与y=(
| 1 |
| 2 |
当直线L到原点的距离大于
| 3 |
∵
| x2 |
| 9 |
| y2 |
| 4 |
∴与圆C相交的直线L一定和椭圆
| x2 |
| 9 |
| y2 |
| 4 |
点评:本题考查椭圆的性质和应用,解题时要熟悉各个函数的图象.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 与圆C相交,则直线
与圆C相交,则直线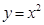 B.
B.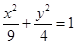 C.
C.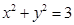 D.
D. 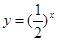
 与圆C
与圆C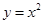 B.
B.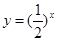
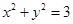 D.
D.