题目内容
函数f(x)在[-3,3]上是减函数,且f(m-1)-f(2m-1)>0,则m的取值范围是________.
(0,2]
分析:先将题中条件:“f(m-1)-f(2m-1)>0”移项得:f(m-1)>f(2m-1),再结合f(x)是定义在[-3,3]上的减函数,脱去符号:“f”,转化为关于m的一元不等式组,最后解得实数m的取值范围,必须注意原函数的定义域范围.
解答:∵f(x)在[-3,3]上是减函数
∴由f(m-1)-f(2m-1)>0,得f(m-1)>f(2m-1)
∵函数f(x)在[-3,3]上是减函数,
∴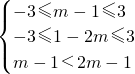 即
即 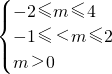
解得 0<m≤2,
∴m的取值范围是(0,2].
点评:本题考查了函数的定义域、函数单调性的性质、函数的单调性的反向应用,考查学生的转化能力,属于基础题.
分析:先将题中条件:“f(m-1)-f(2m-1)>0”移项得:f(m-1)>f(2m-1),再结合f(x)是定义在[-3,3]上的减函数,脱去符号:“f”,转化为关于m的一元不等式组,最后解得实数m的取值范围,必须注意原函数的定义域范围.
解答:∵f(x)在[-3,3]上是减函数
∴由f(m-1)-f(2m-1)>0,得f(m-1)>f(2m-1)
∵函数f(x)在[-3,3]上是减函数,
∴
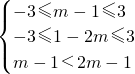 即
即 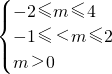
解得 0<m≤2,
∴m的取值范围是(0,2].
点评:本题考查了函数的定义域、函数单调性的性质、函数的单调性的反向应用,考查学生的转化能力,属于基础题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目