题目内容
(本小题满分14分)
已知函数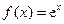 (
(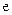 为自然对数的底数),
为自然对数的底数),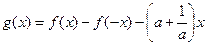 ,
,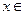
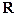 ,
,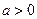 .
.
(1)判断函数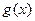 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)求函数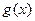 的单调递增区间;
的单调递增区间;
(3)证明:对任意实数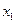 和
和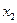 ,且
,且 ,都有不等式
,都有不等式
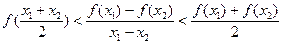 成立.
成立.
已知函数
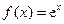 (
(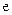 为自然对数的底数),
为自然对数的底数),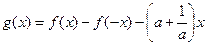 ,
,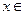
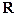 ,
,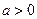 .
.(1)判断函数
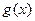 的奇偶性,并说明理由;
的奇偶性,并说明理由;(2)求函数
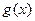 的单调递增区间;
的单调递增区间;(3)证明:对任意实数
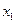 和
和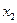 ,且
,且 ,都有不等式
,都有不等式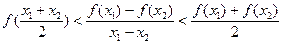 成立.
成立.解: (1)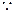 函数
函数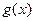 的定义域为
的定义域为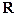 ,
,
且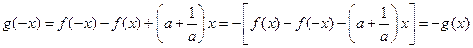
∴函数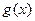 是奇函数. ………………2分
是奇函数. ………………2分
(2)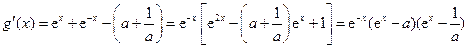
………………3分
当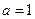 时,
时,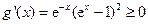 且当且仅当
且当且仅当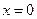 时成立等号,故
时成立等号,故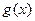 在
在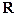 上递增;
上递增;
………………4分
当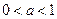 时,
时,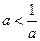 ,令
,令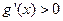 得
得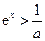 或
或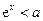 ,
,
故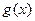 的单调递增区间为
的单调递增区间为 或
或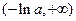 ; ………………5分
; ………………5分
当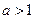 时,
时,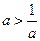 ,令
,令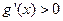 得
得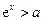 或
或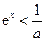 ,
,
故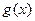 的单调递增区间为
的单调递增区间为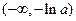 或
或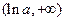 . ………………6分
. ………………6分
(3)不妨设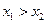 ,
,
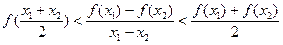
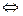
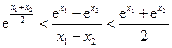 ,
,
 ………………7分
………………7分
令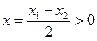 ,则只需证
,则只需证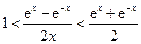 ………………8分
………………8分
先证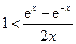 , 由(2)知
, 由(2)知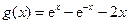 在
在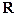 上递增,
上递增,
∴当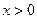 时,
时,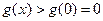
∴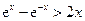 ,从而由
,从而由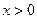 知
知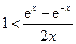 成立; ………………10分
成立; ………………10分
再证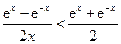 ,即证:
,即证: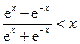 ,
,
令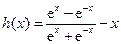 ,则
,则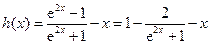 是减函数,
是减函数,
∴当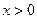 时,
时,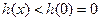 ,从而
,从而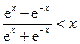 成立. ………………13分
成立. ………………13分
综上,对任意实数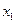 和
和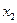 ,且
,且 ,都有不等式
,都有不等式
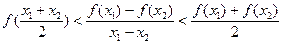 成立. ………………14分
成立. ………………14分
 函数
函数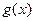 的定义域为
的定义域为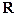 ,
,且
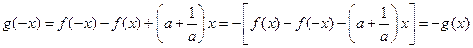
∴函数
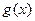 是奇函数. ………………2分
是奇函数. ………………2分(2)
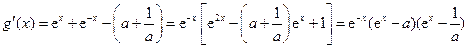
………………3分
当
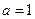 时,
时,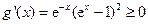 且当且仅当
且当且仅当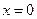 时成立等号,故
时成立等号,故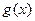 在
在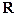 上递增;
上递增;………………4分
当
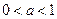 时,
时,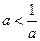 ,令
,令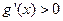 得
得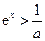 或
或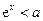 ,
,故
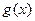 的单调递增区间为
的单调递增区间为 或
或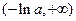 ; ………………5分
; ………………5分当
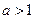 时,
时,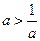 ,令
,令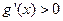 得
得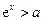 或
或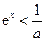 ,
,故
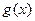 的单调递增区间为
的单调递增区间为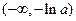 或
或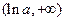 . ………………6分
. ………………6分(3)不妨设
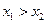 ,
, 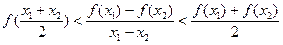
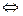
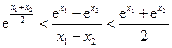 ,
, ………………7分
………………7分 令
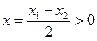 ,则只需证
,则只需证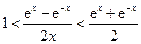 ………………8分
………………8分先证
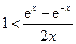 , 由(2)知
, 由(2)知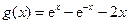 在
在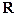 上递增,
上递增,∴当
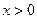 时,
时,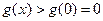
∴
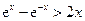 ,从而由
,从而由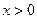 知
知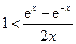 成立; ………………10分
成立; ………………10分再证
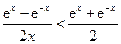 ,即证:
,即证: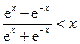 ,
,令
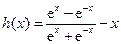 ,则
,则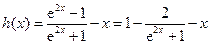 是减函数,
是减函数,∴当
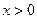 时,
时,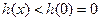 ,从而
,从而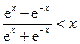 成立. ………………13分
成立. ………………13分综上,对任意实数
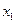 和
和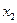 ,且
,且 ,都有不等式
,都有不等式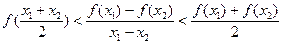 成立. ………………14分
成立. ………………14分略

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目

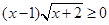 的解集是( )
的解集是( )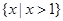 B
B 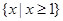 C
C 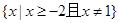 D
D 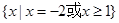
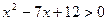 ; (2)
; (2)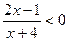 .
.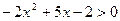 ,化简:
,化简: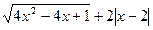
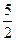 )x<(k2-2k+
)x<(k2-2k+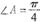 ,
,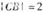 ,设
,设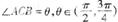 .
. (II)求.
(II)求.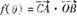 的单调递增区间.
的单调递增区间.

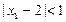 ,
,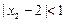 .
.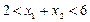 ,
,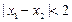 ;
;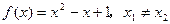 ,求证:
,求证: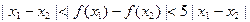 .
.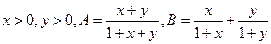 ,则
,则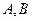 的大小关系是 .
的大小关系是 . 的外接圆,D是的中点,BD交AC于E。
的外接圆,D是的中点,BD交AC于E。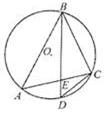
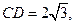 O到AC的距离为1,求⊙O的半径。
O到AC的距离为1,求⊙O的半径。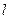 的参数方程为
的参数方程为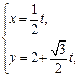 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为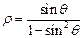 ,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线
,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线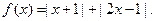
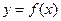 的图象;
的图象;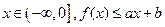 恒成立,求a-b的最大值。
恒成立,求a-b的最大值。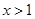 时,
时,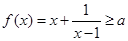 恒成立,则
恒成立,则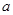 的取值范围为 。
的取值范围为 。