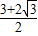题目内容
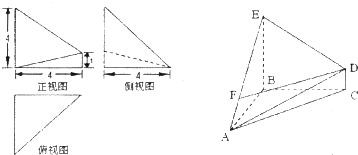
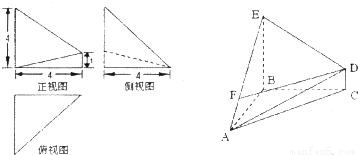
已知几何体A-BCDE的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
(1)若几何体A-BCDE的体积为16,求实数a的值;
(2)若a=1,求异面直线DE与AB所成角的余弦值;
(3)是否存在实数a,使得二面角A-DE-B的平面角是45°,若存在,请求出a值;若不存在请说明理由.

(1)若几何体A-BCDE的体积为16,求实数a的值;
(2)若a=1,求异面直线DE与AB所成角的余弦值;
(3)是否存在实数a,使得二面角A-DE-B的平面角是45°,若存在,请求出a值;若不存在请说明理由.


分析:(1)由该几何体的三视图知AC⊥面BCED,且EC=BC=AC=4,BD=a,由几何体A-BCDE的体积为16,构造关于a的方程解方程可得答案.
(2)求异面直线所成的角,一般有两种方法,
解一是几何法,其基本解题思路是“异面化共面,认定再计算”,即利用平移法和补形法将两条异面直线转化到同一个三角形中,结合余弦定理来求.过点B作BF∥ED交EC于F,连接AF,则∠FBA或其补角即为异面直线DE与AB所成角;
解二是向量法,以C为原点,以CA、CB、CE所在直线为x、y、z轴建立如图所示的空间直角坐标系分别求出异面直线DE与AB的方向向量代入向量夹角公式,可得答案.
(3)以C为原点,以CA、CB、CE所在直线为x、y、z轴建立如图所示的空间直角坐标系,求出平面BDE的法向量和平面ADE的法向量根据二面角A-DE-B的平面角是45°,构造关于a的方程,判断方程是否有解可得答案.
(2)求异面直线所成的角,一般有两种方法,
解一是几何法,其基本解题思路是“异面化共面,认定再计算”,即利用平移法和补形法将两条异面直线转化到同一个三角形中,结合余弦定理来求.过点B作BF∥ED交EC于F,连接AF,则∠FBA或其补角即为异面直线DE与AB所成角;
解二是向量法,以C为原点,以CA、CB、CE所在直线为x、y、z轴建立如图所示的空间直角坐标系分别求出异面直线DE与AB的方向向量代入向量夹角公式,可得答案.
(3)以C为原点,以CA、CB、CE所在直线为x、y、z轴建立如图所示的空间直角坐标系,求出平面BDE的法向量和平面ADE的法向量根据二面角A-DE-B的平面角是45°,构造关于a的方程,判断方程是否有解可得答案.
解答:解:(1)由该几何体的三视图知AC⊥面BCED,
且EC=BC=AC=4,BD=a,
∵几何体A-BCDE的体积为16,
∴V=
•4
=16,
解得a=2;
(2)解一:过点B作BF∥ED交EC于F,连接AF,
则∠FBA或其补角即为异面直线DE与AB所成角,
在△BAF中,AB=4
,BF=AF=
=5,
∴cos∠ABF=
=
;
即异面直线DE与AB所成角的余弦值为
.
解二:以C为原点,以CA、CB、CE所在直线为x、y、z轴建立如图所示的空间直角坐标系,
则A(4,0,0),B(0,4,0),D(0,4,1),E(0,0,4),
得
=(0,-4,3),
=(-4,4,0),
cos<
,
>=
=-
,
又异面直线DE与AB所成角为锐角,
可得异面直线DE与AB所成角的余弦值为
.
(3)以C为原点,以CA、CB、CE所在直线为x、y、z轴建立如图所示的空间直角坐标系,
则A(4,0,0),B(0,4,0),D(0,4,a),E(0,0,4),
平面BDE的法向量
=(1,0,0),
平面ADE的法向量
=(x,y,z),
=(0,-4,4-a),
=(-4,4,a),
由
•
=0,
•
=0,
可得
=(-1,
,1),
cos<
,
>=
=
,
∵a=4.
此时,与正视图为直角梯形条件不符,所以舍去,
因此不存在实数a,使得二面角A-DE-B的平面角是45°.
且EC=BC=AC=4,BD=a,
∵几何体A-BCDE的体积为16,
∴V=
| 1 |
| 3 |
| (a+4)4 |
| 2 |
解得a=2;
(2)解一:过点B作BF∥ED交EC于F,连接AF,
则∠FBA或其补角即为异面直线DE与AB所成角,
在△BAF中,AB=4
| 2 |
| 16+9 |
∴cos∠ABF=
| BF2+AB2-AF2 |
| 2BF•AB |
2
| ||
| 5 |
即异面直线DE与AB所成角的余弦值为
2
| ||
| 5 |
解二:以C为原点,以CA、CB、CE所在直线为x、y、z轴建立如图所示的空间直角坐标系,
则A(4,0,0),B(0,4,0),D(0,4,1),E(0,0,4),
得
| DE |
| AB |
cos<
| DE |
| AB |
| ||||
|
|
2
| ||
| 5 |
又异面直线DE与AB所成角为锐角,
可得异面直线DE与AB所成角的余弦值为
2
| ||
| 5 |
(3)以C为原点,以CA、CB、CE所在直线为x、y、z轴建立如图所示的空间直角坐标系,
则A(4,0,0),B(0,4,0),D(0,4,a),E(0,0,4),
平面BDE的法向量
| n1 |
平面ADE的法向量
| n2 |
| DE |
| AD |
由
| n2 |
| DE |
| n2 |
| AD |
可得
| n2 |
| 4-a |
| 4 |
cos<
| n1 |
| n2 |
| ||||
|
|
| ||
| 2 |
∵a=4.
此时,与正视图为直角梯形条件不符,所以舍去,
因此不存在实数a,使得二面角A-DE-B的平面角是45°.
点评:本题考查的知识点是与二面角有关的立体几何综合应用,由三视图求面积,异面直线及其所成的角,难度比较大,熟练掌握几何法及向量法求夹角的方法和步骤是解答本题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
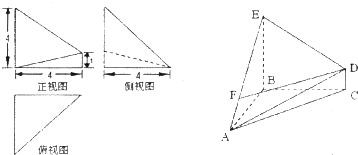
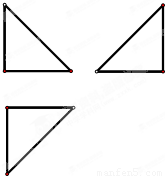
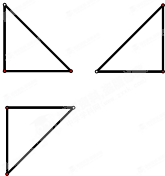 已知几何体A-BCD的三视图如图所示,其中每个图形都是腰长为1的等腰直角三角形,则该几何体的表面积为( )
已知几何体A-BCD的三视图如图所示,其中每个图形都是腰长为1的等腰直角三角形,则该几何体的表面积为( )