题目内容
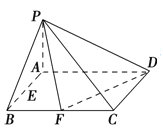
【题目】已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
(1)证明:PF⊥FD;
(2)判断并说明PA上是否存在点G,使得EG∥平面PFD;
(3)若PB与平面ABCD所成的角为45°,求二面角A-PD-F的余弦值.
【答案】(1)详见解析;(2)详见解析;(3)![]() .
.
【解析】
(1)因为PA⊥平面ABCD,∠BAD=90°,AB=1,AD=2,建立如图所示的空间直角坐标系,则A(0,0,0),B(1,0,0),F(1,1,0),D(0,2,0).

不妨令P(0,0,t),则![]() =(1,1,-t),
=(1,1,-t),![]() =(1,-1,0).
=(1,-1,0).
所以![]() ·
·![]() =1×1+1×(-1)+(-t)×0=0,所以PF⊥FD.
=1×1+1×(-1)+(-t)×0=0,所以PF⊥FD.
(2)设平面PFD的法向量为n=(x,y,z),由(1)知![]() =(1,1,-t),
=(1,1,-t),![]() =(1,-1,0),则由
=(1,-1,0),则由 ,得
,得![]() ,令z=1,则x=y=
,令z=1,则x=y=![]() .
.
故n=![]() 是平面PFD的一个法向量.
是平面PFD的一个法向量.
设G点坐标为(0,0,m),因为E![]() ,则
,则![]()
要使EG∥平面PFD,只需![]() ·n=0.即
·n=0.即![]() ×
×![]() +0×
+0×![]() +m×1=m-
+m×1=m-![]() =0,
=0,
所以m=![]() t,从而PA上满足AG=
t,从而PA上满足AG=![]() AP的点G可使得EG∥平面PFD.
AP的点G可使得EG∥平面PFD.
(3)易知AB⊥平面PAD,所以![]() =(1,0,0)是平面PAD的一个法向量.
=(1,0,0)是平面PAD的一个法向量.
又因为PA⊥平面ABCD,所以∠PBA是PB与平面ABCD所成的角,故∠PBA=45°,所以PA=1,则平面PFD的一个法向量为n=![]() ,
,
则cos〈![]() ,n〉=
,n〉=![]() =
= =
=![]() ,
,
由题图可判断二面角为锐角.故所求二面角A-PD-F的余弦值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目