题目内容
设函数f(x)=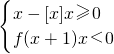 其中[x]表示不超过x的最大整数,如[-1.3]=-2,[1.3]=1,则函数y=f(x)-
其中[x]表示不超过x的最大整数,如[-1.3]=-2,[1.3]=1,则函数y=f(x)- x-
x- 不同零点的个数
不同零点的个数
- A.2
- B.3
- C.4
- D.5
B
分析:根据函数f(x)的解析式的意义,分别画出函数y=f(x)、y=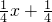 的图象,可求出其交点,即为所求函数的零点.
的图象,可求出其交点,即为所求函数的零点.
解答:f(x)=x-[x](x≥0)表示的是实数x的小数部分,∴(x-[x])∈[0,1);当x∈[-1,0)时,(x+1)∈[0,1),又f(x)=f(x+1),为周期函数.
据此分别作出函数y=f(x)、y=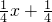 的图象,如图所示:
的图象,如图所示: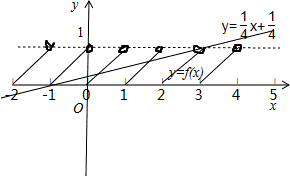
可以看出:函数f(x)与函数y=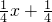 的图象只有3个交点.
的图象只有3个交点.
即函数y=f(x)- x-
x- 不同零点的个数为3.
不同零点的个数为3.
故选B.
点评:正确理解函数f(x)的表达式的意义和画出图象是解题的关键.
分析:根据函数f(x)的解析式的意义,分别画出函数y=f(x)、y=
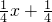 的图象,可求出其交点,即为所求函数的零点.
的图象,可求出其交点,即为所求函数的零点.解答:f(x)=x-[x](x≥0)表示的是实数x的小数部分,∴(x-[x])∈[0,1);当x∈[-1,0)时,(x+1)∈[0,1),又f(x)=f(x+1),为周期函数.
据此分别作出函数y=f(x)、y=
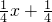 的图象,如图所示:
的图象,如图所示: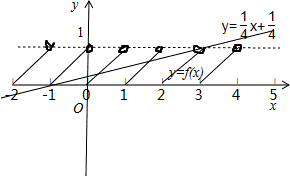
可以看出:函数f(x)与函数y=
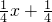 的图象只有3个交点.
的图象只有3个交点.即函数y=f(x)-
 x-
x- 不同零点的个数为3.
不同零点的个数为3.故选B.
点评:正确理解函数f(x)的表达式的意义和画出图象是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 其中[x]表示不超过x的最大整数,如[-1.3]=-2,[1.3]=1,则函数y=f(x)-
其中[x]表示不超过x的最大整数,如[-1.3]=-2,[1.3]=1,则函数y=f(x)- x-
x- 不同零点的个数( )
不同零点的个数( )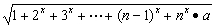 其中a∈R,n是任意给定的自然数,n≥2,如果在x∈(-∞,1]上有意义,求a的取值范围.
其中a∈R,n是任意给定的自然数,n≥2,如果在x∈(-∞,1]上有意义,求a的取值范围. •
• 其中向量
其中向量 =(2cosx,1),
=(2cosx,1), .
.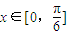 时,f(x)的最大值为4,求m的值.
时,f(x)的最大值为4,求m的值.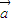 •
•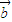 其中向量
其中向量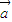 =(2cosx,1),
=(2cosx,1),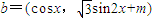 .
.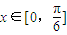 时,f(x)的最大值为4,求m的值.
时,f(x)的最大值为4,求m的值.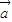 •
• 其中向量
其中向量 =(2cosx,1),
=(2cosx,1), .
.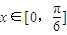 时,f(x)的最大值为4,求m的值.
时,f(x)的最大值为4,求m的值.