题目内容
直线y=kx与双曲线
-
=1的左右两支都有交点的充要条件是k∈(-1,1),且该双曲线与直线y=
x-
相交所得弦长为
,则该双曲线方程为 .
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
| 2 |
4
| ||
| 3 |
分析:直线y=kx与双曲线
-
=1的左右两支都有交点的充要条件是k∈(-1,1),可得
=1.设双曲线的方程为x2-y2=m.与直线方程联立,利用弦长公式即可得出m.
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
解答:解:∵直线y=kx与双曲线
-
=1的左右两支都有交点的充要条件是k∈(-1,1),
∴
=1.
设双曲线的方程为x2-y2=m.
联立
,化为3y2+12y+9-m=0.
∵直线与双曲线有两个交点,∴△=122-12(9-m)>0,解得m>-3.
∴y1+y2=-4,y1y2=3-
.
∴
=
=
,
化为m=1.满足△>0.
因此双曲线的方程为:x2-y2=1.
故答案为:x2-y2=1.
| x2 |
| a2 |
| y2 |
| b2 |
∴
| b |
| a |
设双曲线的方程为x2-y2=m.
联立
|
∵直线与双曲线有两个交点,∴△=122-12(9-m)>0,解得m>-3.
∴y1+y2=-4,y1y2=3-
| m |
| 3 |
∴
| (1+4)[(y1+y2)2-4y1y2] |
5[42-4×(3-
|
4
| ||
| 3 |
化为m=1.满足△>0.
因此双曲线的方程为:x2-y2=1.
故答案为:x2-y2=1.
点评:本题考查了双曲线的标准方程及其性质、直线与双曲线相交转化为方程联立得到根与系数的关系、弦长公式等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
设双曲线
-
=1(a>0,b>0)的半焦距为c,离心率为
.若直线y=kx与双曲线的一个交点的横坐标恰为c,则k等于( )
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| 4 |
A、±
| ||
B、±
| ||
C、±
| ||
D、±
|
 的左右两支各有一个交点,则k的取值范围是( )
的左右两支各有一个交点,则k的取值范围是( )


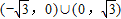
 的半焦距为c,离心率为
的半焦距为c,离心率为 .若直线y=kx与双曲线的一个交点的横坐标恰为c,则k等于( )
.若直线y=kx与双曲线的一个交点的横坐标恰为c,则k等于( )


