题目内容
(08年温州八校适应性考试三) (14分)如图,正三棱柱![]() 中,
中,![]() 是
是![]() 中点.AB=2
中点.AB=2
(Ⅰ)求证:![]() //平面
//平面![]() ;
;
(Ⅱ) 当![]() 为何值时,二面角
为何值时,二面角![]() 的正弦值为
的正弦值为![]() ?
?

解析:(Ⅰ) 连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
在![]() 中,
中,![]()
![]() 分别为
分别为![]() 中点,
中点,![]()
![]() .
.
![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() . …………(6分)
. …………(6分)
(Ⅱ) 法一:过![]() 作
作![]() 于
于![]() ,由三垂线定理得
,由三垂线定理得![]() ,
,
故∠![]() 为二面角
为二面角![]() 的平面角. ……………………………………(9分)
的平面角. ……………………………………(9分)
令![]() ,则
,则![]() ,又
,又![]() ,
,
在![]() △
△![]() 中,
中,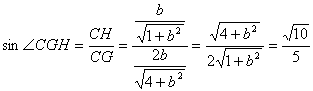 ,
,
解得![]() 。
。
![]() 当
当![]() 时,二面角
时,二面角![]() 的正弦值为
的正弦值为![]() . ……………………(14分)
. ……………………(14分)
法二:设![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() ,
,
以![]() 为坐标原点建立空间直角坐标系,如右图所示:
为坐标原点建立空间直角坐标系,如右图所示:
则![]() ,
,
则![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,
,
则有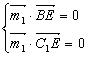 ,
,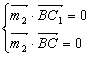 ,即
,即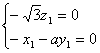 ,
,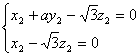 ,
,
设![]() ,则
,则![]() ,
,
![]()
![]()
![]()
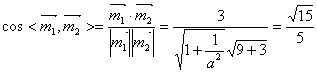 ,解得
,解得![]() .
.
![]() 即当
即当![]() 时,二面角
时,二面角![]() 的正弦值为
的正弦值为![]() . …………………(14分)
. …………………(14分)


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目