题目内容
(1)解不等式组: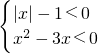
(2)求下列函数的反函数: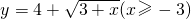 .
.
解:(1)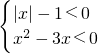 ?
?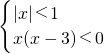 ?
?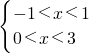
∴0<x<1,原不等式的解集是:(0,1)
(2)为了求反函数,将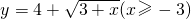 变形为
变形为

∴3+x=(y-4)2,其中y≥4
即x=(y-4)2-3,(y≥4)
∴反函数为f-1(x)=(x-4)2-3,(x≥4)
分析:(1)对于不等式组中的第一个不等式,可以利用绝对值不等式的解法得到-1<x<1,再根据一元二次不等式的解法,得到第二个不等式的解集为{x|0<x<3},最后取交集可得原不等式的解集;
(2)将原函数变形:先移项,再两边平方,可得3+x=(y-4)2,最后将x、y互换,得到反函数的表达式为
f-1(x)=(x-4)2-3,根据平方大于或等于0,得到反函数的定义域.
点评:本题第一小问考查了不等式的解法,第二小问考查了反函数的求法,都属于基础题.求函数的反函数时,应该注意必须交待反函数的自变量的取值范围,否则解题不算完整.
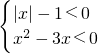 ?
?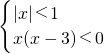 ?
?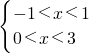
∴0<x<1,原不等式的解集是:(0,1)
(2)为了求反函数,将
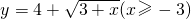 变形为
变形为
∴3+x=(y-4)2,其中y≥4
即x=(y-4)2-3,(y≥4)
∴反函数为f-1(x)=(x-4)2-3,(x≥4)
分析:(1)对于不等式组中的第一个不等式,可以利用绝对值不等式的解法得到-1<x<1,再根据一元二次不等式的解法,得到第二个不等式的解集为{x|0<x<3},最后取交集可得原不等式的解集;
(2)将原函数变形:先移项,再两边平方,可得3+x=(y-4)2,最后将x、y互换,得到反函数的表达式为
f-1(x)=(x-4)2-3,根据平方大于或等于0,得到反函数的定义域.
点评:本题第一小问考查了不等式的解法,第二小问考查了反函数的求法,都属于基础题.求函数的反函数时,应该注意必须交待反函数的自变量的取值范围,否则解题不算完整.

练习册系列答案
相关题目
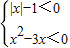
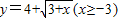 .
.