题目内容
已知二次函数f(x)=ax2+bx+1的导函数 为f′(x),f′(0)>0,f(x)与x轴恰有一个交点,则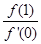 的最小值为
的最小值为
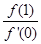 的最小值为
的最小值为 A.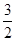 | B.2 | C.3 | D.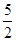 |
B
试题分析:解:∵f(x)=ax2+bx+1,∴f′(x)=2ax+b,∴f′(0)=b,又f′(0)>0,∴b>0.又已知f(x)与x轴恰有一个交点,∴△=b2-4a=0,则可知f(1)=a+b+1=
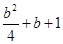 ,则
,则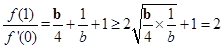 ,故选B.
,故选B.点评:本题综合考查了二次函数、导数、基本不等式,熟练掌握它们的性质及使用方法是解决问题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
 的解集为
的解集为 ,则
,则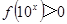 的解集为( )
的解集为( )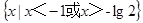
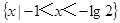
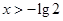 }
}  }
}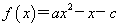 ,且
,且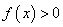 的解集为(-2,1),则函数
的解集为(-2,1),则函数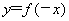 的图象为( )
的图象为( )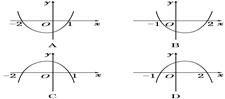
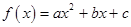 .
.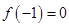 ,试判断函数
,试判断函数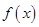 零点个数;
零点个数;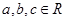 ,使
,使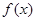 同时满足以下条件
同时满足以下条件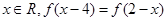 ,且
,且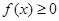 ;
;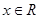 ,都有
,都有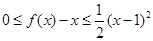 。若存在,求出
。若存在,求出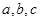 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。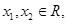 且
且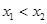 ,
,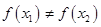 ,试证明存在
,试证明存在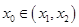 ,
,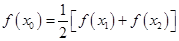 成立。
成立。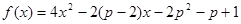 在区间
在区间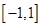 内至少存在一数值
内至少存在一数值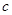 ,使
,使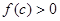 ,则实数
,则实数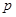 的取值范围是______________________.
的取值范围是______________________.  的解是
的解是 ,则m-n的值是
,则m-n的值是

 的值域为
的值域为 ,则
,则 的取值范围是( )
的取值范围是( )


