题目内容
设随机变量的概率分布如下表所示,且其数学期望E(X)=3.则表中这个随机变量的方差是
1
1
.| X | 1 | 2 | 3 | 4 | ||||
| P |
|
a | b |
|
分析:先根据概率分布表,利用概率之和为1和期望的计算公式求出a,b,再直接利用方差公式计算即可.
解答:解:由于概率之和为1,
∴a+b=1-(
+
)=
.又E(X)=
×1+a×2+b×3+
×4=3,两式联立解得a=
,b=
.
随机变量的方差是
×(1-3)2+
×(2-3)2+
×(3-3)2+
×(4-3)2=1
故答案为:1.
∴a+b=1-(
| 1 |
| 8 |
| 3 |
| 8 |
| 1 |
| 2 |
| 1 |
| 8 |
| 3 |
| 8 |
| 1 |
| 8 |
| 3 |
| 8 |
随机变量的方差是
| 1 |
| 8 |
| 1 |
| 8 |
| 3 |
| 8 |
| 3 |
| 8 |
故答案为:1.
点评:本题主要考查离散型随机变量的分布和数学期望、方差等基础知识,熟记期望、方差的公式是解题的关键.

练习册系列答案
相关题目
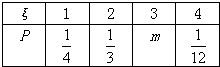 设随机变量ξ的概率分布如表所示:
设随机变量ξ的概率分布如表所示: