Question

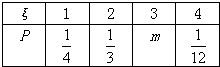设随机变量ξ的概率分布如表所示：
求：（l）P（ξ＜1），P（ξ≤1），P（ξ＜2），P（ξ≤2）；
（2）P（x）=P（ξ≤x），x∈R．

Answer 1

分析：（1）根据所给的分布列，首先根据分布列中概率之和是1，做出分布列中出现的字母m的值，根据所要求的不同变量的范围写出对应的概率的值．
（2）要求把概率表示成函数的形式，看清条件中出现的变量的值，写出不同的分段，注意分段时概率知相同的变量要分在一段，写出分段函数．

解答：解：（1）根据所给的分布列可知

1

4

+

1

3

+m+

1

12

=1，
∴m=

1

3

，
∴P（ξ＜1）=0
P（ξ≤1）=P（ξ=1）=

1

4

P（ξ＜2）=P（ξ≤1）=P（ξ=1）=

1

4

P（ξ≤2）=P（ξ=1）+P（ξ=2）=

1

4

+

1

3

=

7

12

（2）根据所给的分布列和第一问做出的结果，
得到P（X）=

1

4

，（x≤1）
P（X）=

7

12

，（1＜X≤2）
P（X）=

11

12

，（2＜x≤3）
p（X）=1，（X≥3）

点评：本题考查离散型随机变量的分布列，考查画出数据的概率，考查用函数形式变式变量的分布列，考查分段函数的写法，本题是一个综合题目．