题目内容
一个均匀的正四面体面上分别涂有1、2、3、4四个数字,现随机投掷两次,正四面体面朝下的数字分别为b、c.若方程x2-bx-c=0至少有一根a∈{1,2,3,4},就称该方程为“漂亮方程”,方程为“漂亮方程”的概率为
.
| 3 |
| 16 |
| 3 |
| 16 |
分析:分类讨论方程根分别为1,2,3,4时,基本事件的个数,然后代入古典概型公式即可得到结果.
解答:解:(Ⅱ)①若方程一根为x=1,则1-b-c=0,即b+c=1,不成立.
②若方程一根为x=2,则4-2b-c=0,即2b+c=4,所以,
.
③若方程一根为x=3,则9-3b-c=0,即3b+c=9,所以,
.
④若方程一根为x=4,则16-4b-c=0,即4b+c=16,所以,
.
综合①②③④知,(b,c)的所有可能取值为(1,2)、(2,3)、(3,4),
所以,“漂亮方程”共有3个,方程为“漂亮方程”的概率p=
,
故答案为
.
②若方程一根为x=2,则4-2b-c=0,即2b+c=4,所以,
|
③若方程一根为x=3,则9-3b-c=0,即3b+c=9,所以,
|
④若方程一根为x=4,则16-4b-c=0,即4b+c=16,所以,
|
综合①②③④知,(b,c)的所有可能取值为(1,2)、(2,3)、(3,4),
所以,“漂亮方程”共有3个,方程为“漂亮方程”的概率p=
| 3 |
| 16 |
故答案为
| 3 |
| 16 |
点评:本题考查的知识是等可能性事件的概率,求出基本事件的总数和满足某个事件的基本事件个数是解答本题
的关键,属于中档题.
的关键,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
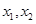 ,记
,记 .
. 取得最大值和最小值时的概率; (2)求
取得最大值和最小值时的概率; (2)求