Question

若一个等差数列前3项的和为34，最后3项的和为146，且所有项的和为390，则这个数列的项数是       。

 

Answer 1

【答案】

13

【解析】

试题分析：先根据题意求出a₁+a_n的值，再把这个值代入求和公式，进而求出数列的项数n．根据题意可知解：依题意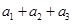 =34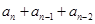， =146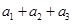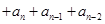，∴ =34+146=180，又∵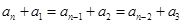=∴、=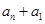 =60，∴S_n=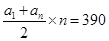 ∴n=13，故填写13.

考点：等差数列的求和公式

点评：本题主要考查了等差数列中的求和公式的应用，属于基础题