题目内容
(1)求过点A(2,0)且与⊙B:(x+2)2+y2=36内切的圆的圆心的轨迹方程.
(2)设点P是(1)题中的轨迹上的动点,已知定点D(1,1),求|PD|+
|PA|的最小值.
(2)设点P是(1)题中的轨迹上的动点,已知定点D(1,1),求|PD|+
| 3 | 2 |
分析:(1)根据题意,先得到圆B的圆心为B(-2,0),半径为6,设动圆圆心为M(x,y),切⊙B于点C,由内切两圆的性质,结合圆M的半径进行等量代换,可推出动点M到两个定点A、B的距离之和为定值6,得到所求轨迹是以A、B两点为焦点的椭圆,再根据题中所给数据得到它的方程.
(2)先用圆锥曲线的统一定义,表示出P到右焦点与右准线距离的关系,求得
|PA|等于点P到右准线的距离|PN|,再结合平面几何垂线段最短的原理,进而推断出|PD|+
|PA|最小值为点D到右准线的距离,不难求得此时的距离最小值.
(2)先用圆锥曲线的统一定义,表示出P到右焦点与右准线距离的关系,求得
| 3 |
| 2 |
| 3 |
| 2 |
解答:解:(1)∵圆的方程为⊙B:(x+2)2+y2=36
∴圆心为B(-2,0),半径r=6.
设动圆圆心为M(x,y),切点为C,依题意,
∵动圆与⊙B:(x+2)2+y2=36内切
∴|BC|-|MC|=|BM|,而|BC|=6,
∴|BM|+|CM|=6.
又∵点A和C都在圆M上
∴|CM|=|AM|,可得|BM|+|AM|=6.
所以,M的轨迹是以A、B为焦点的椭圆,其中2a=6,得a=3,
而c=2,所以b2=a2-c2=5,椭圆方程为:
+
=1;
(2)根据题意,定点D(1,1)在椭圆
+
=1内,连接PD,过P点作PN⊥l(l为右准线)于N点,
右准线方程为:x=
,即x=
.
由圆锥曲线的统一定义可知,
=e=
,⇒
|PA|=|PN|.…(8分)
过点D作DG⊥l于G 点,交椭圆于Q点.
由平面几何知识,可得|PD|+
|PA|=|PD|+|PN|≥|DQ|+|QG|=|DG|=
-1=
∴|PD|+
|PA|的最小值为
.…(13分)
∴圆心为B(-2,0),半径r=6.
设动圆圆心为M(x,y),切点为C,依题意,
∵动圆与⊙B:(x+2)2+y2=36内切
∴|BC|-|MC|=|BM|,而|BC|=6,
∴|BM|+|CM|=6.
又∵点A和C都在圆M上
∴|CM|=|AM|,可得|BM|+|AM|=6.
所以,M的轨迹是以A、B为焦点的椭圆,其中2a=6,得a=3,
而c=2,所以b2=a2-c2=5,椭圆方程为:
| x2 |
| 9 |
| y2 |
| 5 |
(2)根据题意,定点D(1,1)在椭圆
| x2 |
| 9 |
| y2 |
| 5 |
右准线方程为:x=
| a2 |
| c |
| 9 |
| 2 |
由圆锥曲线的统一定义可知,
| |PA| |
| |PN| |
| 2 |
| 3 |
| 3 |
| 2 |
过点D作DG⊥l于G 点,交椭圆于Q点.
由平面几何知识,可得|PD|+
| 3 |
| 2 |
| 9 |
| 2 |
| 7 |
| 2 |
∴|PD|+
| 3 |
| 2 |
| 7 |
| 2 |
点评:本题借助一个特殊的轨迹为例,主要考查了椭圆的定义和简单几何性质,以及圆锥曲线的统一定义,考查了考生分析问题和解决问题的能力,属于中档题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
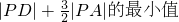 .
. ,0)的⊙C的切线方程;
,0)的⊙C的切线方程;