题目内容
【题目】已知集合![]() 是集合
是集合![]()
![]() 的一个含有
的一个含有![]() 个元素的子集.
个元素的子集.
(Ⅰ)当![]() 时,
时,
设![]()
(i)写出方程![]() 的解
的解![]() ;
;
(ii)若方程![]() 至少有三组不同的解,写出
至少有三组不同的解,写出![]() 的所有可能取值.
的所有可能取值.
(Ⅱ)证明:对任意一个![]() ,存在正整数
,存在正整数![]() 使得方程
使得方程![]()
![]() 至少有三组不同的解.
至少有三组不同的解.
【答案】(Ⅰ)(![]() )
)![]() ,(
,(![]() )
)![]() ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
【解析】试题分析:(Ⅰ)(![]() )利用列举法可得方程
)利用列举法可得方程![]() 的解有:
的解有: ![]() ;(
;(![]() )列出集合
)列出集合![]() 的从小到大
的从小到大![]() 个数中相邻两数的差,中间隔一数的两数差,中间相隔二数的两数差,…中间隔一数的两数差,可发现只有
个数中相邻两数的差,中间隔一数的两数差,中间相隔二数的两数差,…中间隔一数的两数差,可发现只有![]() 出现
出现![]() 次,
次, ![]() 出现
出现![]() 次,其余都不超过
次,其余都不超过![]() 次,从而可得结果;(Ⅱ)不妨设
次,从而可得结果;(Ⅱ)不妨设![]() 记
记![]() ,
,![]()
![]() ,共
,共![]() 个差数,假设不存在满足条件的
个差数,假设不存在满足条件的![]() ,根据
,根据![]() 的取值范围可推出矛盾,假设不成立,从而可得结论.
的取值范围可推出矛盾,假设不成立,从而可得结论.
假设不存在满足条件的![]() ,则这
,则这![]() 个数中至多两个
个数中至多两个![]() 、两个
、两个![]() 、两个
、两个![]() 、两个
、两个![]() 、两个
、两个![]() 、两个
、两个![]() ,.
,.
试题解析:(Ⅰ)(![]() )方程
)方程![]() 的解有:
的解有: ![]()
(![]() )以下规定两数的差均为正,则:
)以下规定两数的差均为正,则:
列出集合![]() 的从小到大
的从小到大![]() 个数中相邻两数的差:
个数中相邻两数的差: ![]() ;
;
中间隔一数的两数差(即上一列差数中相邻两数和):4,5,6,6,5,4;
中间相隔二数的两数差: ![]() ;
;
中间相隔三数的两数差: ![]() ;
;
中间相隔四数的两数差: ![]() ;
;
中间相隔五数的两数差: ![]() ;
;
中间隔一数的两数差: ![]() .
.
这![]() 个差数中,只有
个差数中,只有![]() 出现
出现![]() 次,
次, ![]() 出现
出现![]() 次,其余都不超过
次,其余都不超过![]() 次,
次,
所以![]() 的可能取值有
的可能取值有![]() .
.
(Ⅱ)证明:不妨设![]()
记![]() ,
,![]()
![]() ,共
,共![]() 个差数.
个差数.
假设不存在满足条件的![]() ,则这
,则这![]() 个数中至多两个
个数中至多两个![]() 、两个
、两个![]() 、两个
、两个![]() 、两个
、两个![]() 、两个
、两个![]() 、两个
、两个![]() ,从而
,从而
![]()
![]()
又![]()
![]()
![]()
这与![]() 矛盾,所以结论成立.
矛盾,所以结论成立.

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目,若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.
某学校为了了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有8人 | 8 | 8 | 4 | 2 | 1 | 1 |
选考方案待确定的有6人 | 4 | 3 | 0 | 1 | 0 | 0 | |
女生 | 选考方案确定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 |
选考方案待确定的有6人 | 5 | 4 | 1 | 0 | 0 | 1 |
(Ⅰ)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?
(Ⅱ)假设男生、女生选择选考科目是相互独立的.从选考方案确定的8位男生随机选出1人,从选考方案确定的10位女生中随机选出1人,试求该男生和该女生的选考方案中都含有历史科目的概率;
(Ⅲ)从选考方案确定的8名男生随机选出2名,设随机变量两名男生选考方案相同时![]() ,两名男生选考方案不同时
,两名男生选考方案不同时![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并求出函数![]() 的解析式;
的解析式;
(2)把![]() 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,求
的图象,求![]() 的值.
的值.
【题目】大连市某企业为确定下一年投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位:![]() )和年利润
)和年利润![]() (单位:千元)的影响,对近8年的年宣传费
(单位:千元)的影响,对近8年的年宣传费![]() 和年销售量
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.

|
|
|
|
|
|
|
46.6 | 573 | 6.8 | 289.8 | 1.6 | 215083.4 | 31280 |
表中![]() ,
,![]() .
.
根据散点图判断,
![]() 与
与![]() 哪一个适宜作为年销售量
哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
![]() 根据
根据![]() 的判断结果及表中数据,建立
的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
![]() 已知这种产品的年利润
已知这种产品的年利润![]() 与
与![]() 、
、![]() 的关系为
的关系为![]() .根据
.根据![]() 的结果回答下列问题:
的结果回答下列问题:
![]() 年宣传费
年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
![]() 年宣传费
年宣传费![]() 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
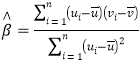 ,
,![]() .
.