题目内容
已知四面体ABCD中,AB=AD=6,AC=4,CD=2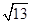 ,AB⊥平面ACD,则四面体 ABCD外接球的表面积为( )
,AB⊥平面ACD,则四面体 ABCD外接球的表面积为( )
| A.36π | B.88π | C.92π | D.128π |
B
解析试题分析:在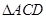 中,由
中,由 ,可得
,可得 ,则
,则 ,又
,又 ,故
,故 ,则
,则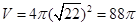 .
.
考点:几何体的组合

练习册系列答案
相关题目
如图是一个几何体的三视图,正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图,则该几何体的全面积为( )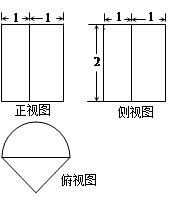
A.2+3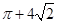 | B.2+2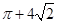 | C.8+5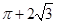 | D.6+3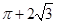 |
空间几何体的三视图如所示,则该几何体的体积为 ( )
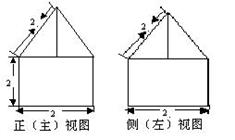
A. | B.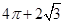 | C.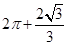 | D. |
某几何体的三视图如图所示,则这个几何体的体积为( )
A. | B. | C. | D. |
已知直三棱柱 的6个顶点都在球
的6个顶点都在球 的球面上,若
的球面上,若
 ,
, ,则球
,则球 的半径为 ( )
的半径为 ( )
A. | B. | C. | D. |
如果一个几何体的三视图如图所示(单位长度: cm), 则此几何体的表面积是( )
A. | B.21 | C. | D.24 |
已知正方体的外接球的体积是 ,则这个正方体的棱长是( )
,则这个正方体的棱长是( )
A. | B. | C. | D. |
棱长都相等的一个正四面体 和一个正八面体
和一个正八面体 ,把它们拼起来,使面
,把它们拼起来,使面 重合,则所得多面体是( )
重合,则所得多面体是( )
| A.七面体 | B.八面体 | C.九面体 | D.十面体 |



