题目内容
 长方体ABCD-A1B1C1D1中,AA1=
长方体ABCD-A1B1C1D1中,AA1=| 2 |
(Ⅰ)求证:B1D1∥平面BC1D;
(Ⅱ)求证:A1O⊥平面BC1D.
分析:(Ⅰ)欲证B1D1∥平面BC1D,根据直线与平面平行的判定定理可知只需证B1D1与平面BC1D内一直线平行,而B1D1∥BD,且B1D1在平面BC1D外,满足定理所需条件;
(Ⅱ)欲证A1O⊥平面BC1D,根据直线与平面垂直的判定定理可知只需证A1O与平面BC1D内两相交直线垂直,连接OC1
,根据线面垂直的性质可知A1O⊥BD,根据勾股定理可知A1O⊥OC1,满足定理所需条件.
(Ⅱ)欲证A1O⊥平面BC1D,根据直线与平面垂直的判定定理可知只需证A1O与平面BC1D内两相交直线垂直,连接OC1
,根据线面垂直的性质可知A1O⊥BD,根据勾股定理可知A1O⊥OC1,满足定理所需条件.
解答: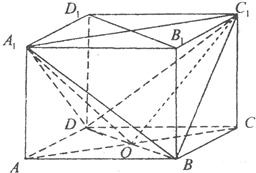 (Ⅰ)证明:依题意:B1D1∥BD,且B1D1在平面BC1D外.(2分)
(Ⅰ)证明:依题意:B1D1∥BD,且B1D1在平面BC1D外.(2分)
∴B1D1∥平面BC1D(4分)
(Ⅱ)证明:连接OC1
∵BD⊥AC,AA1⊥BD
∴BD⊥平面ACC1A1(5分)
又∵O在AC上,∴A1O在平面ACC1A1上
∴A1O⊥BD(6分)
∵AB=BC=2∴AC=A1C1=2
∴OA=
∴Rt△AA1O中,A1O=
=2(7分)
同理:OC1=2
∵△A1OC1中,A1O2+OC12=A1C12
∴A1O⊥OC1(8分)
∴A1O⊥平面BC1D
 (Ⅰ)证明:依题意:B1D1∥BD,且B1D1在平面BC1D外.(2分)
(Ⅰ)证明:依题意:B1D1∥BD,且B1D1在平面BC1D外.(2分)∴B1D1∥平面BC1D(4分)
(Ⅱ)证明:连接OC1
∵BD⊥AC,AA1⊥BD
∴BD⊥平面ACC1A1(5分)
又∵O在AC上,∴A1O在平面ACC1A1上
∴A1O⊥BD(6分)
∵AB=BC=2∴AC=A1C1=2
| 2 |
∴OA=
| 2 |
∴Rt△AA1O中,A1O=
| AA12+OA2 |
同理:OC1=2
∵△A1OC1中,A1O2+OC12=A1C12
∴A1O⊥OC1(8分)
∴A1O⊥平面BC1D
点评:本题考查直线与平面平行的判定,直线与平面垂直的判定,考查学生空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
长方体ABCD-A1B1C1D1中,AB=3,BC=4,AA1=5 则三棱锥A1-ABC的体积为( )
| A、10 | B、20 | C、30 | D、35 |
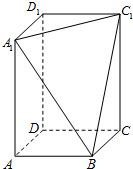 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.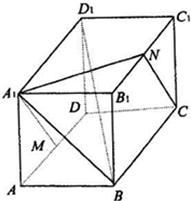 如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC=
如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC= 如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.
如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点. 在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.
在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.