题目内容
已知a>0,且a≠1,数列{an}的前n项和为Sn,它满足条件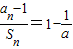 .数列{bn}中,bn=an•lgan.
.数列{bn}中,bn=an•lgan.(1)求数列{bn}的前n项和Tn;
(2)若对一切n∈N*都有bn<bn+1,求a的取值范围.
【答案】分析:(1)由题意知,a1=a,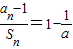 转化为:
转化为: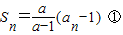 ,
,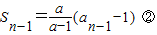 ,①-②,得
,①-②,得  ,由此能求出数列{an}的通项公式.
,由此能求出数列{an}的通项公式.
(2)由bn=an•lgan,知bn=nanlga,当对一切n∈N+,都有bn<bn-1,即有nanlga<(n+1)an-1lga,由此进行分类讨论,能够得到a的取值范围.
解答:解:(1)由题意知,当n=1时,a1=a,
当n≥2时, ,
,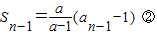 ,
,
①-②,得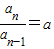 ,
,
∴数列{an}是等比数列,
∴an=an(n∈N+).
(2)∵bn=an•lgan,
∴bn=nanlga,
当对一切n∈N+,都有bn<bn-1,
即有nanlga<(n+1)an-1lga,
当lga>0,即a>1时,a>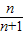 对一切n∈N+都成立,∴a>1.
对一切n∈N+都成立,∴a>1.
当lga<0,即0时,有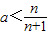 对一切n∈N+都成立,∴
对一切n∈N+都成立,∴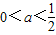 .
.
综上所述a>1或 .
.
点评:本题考查数列的通项公式和数列与不等式的综合运用,解题时要认真审题,注意分类讨论思想的合理运用.
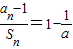 转化为:
转化为: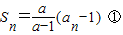 ,
,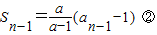 ,①-②,得
,①-②,得  ,由此能求出数列{an}的通项公式.
,由此能求出数列{an}的通项公式.(2)由bn=an•lgan,知bn=nanlga,当对一切n∈N+,都有bn<bn-1,即有nanlga<(n+1)an-1lga,由此进行分类讨论,能够得到a的取值范围.
解答:解:(1)由题意知,当n=1时,a1=a,
当n≥2时,
 ,
,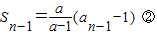 ,
,①-②,得
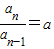 ,
,∴数列{an}是等比数列,
∴an=an(n∈N+).
(2)∵bn=an•lgan,
∴bn=nanlga,
当对一切n∈N+,都有bn<bn-1,
即有nanlga<(n+1)an-1lga,
当lga>0,即a>1时,a>
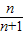 对一切n∈N+都成立,∴a>1.
对一切n∈N+都成立,∴a>1.当lga<0,即0时,有
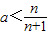 对一切n∈N+都成立,∴
对一切n∈N+都成立,∴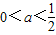 .
.综上所述a>1或
 .
.点评:本题考查数列的通项公式和数列与不等式的综合运用,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
 .
. .
.