题目内容
已知a>0,且a≠1,设p:函数y=loga(x+1)在x∈(0,+∞)内单调递减;q:函数y=x2+(2a-3)x+1有两个不同零点,如果p和q有且只有一个正确,求a的取值范围.
【答案】分析:先由对数函数的单调性求出命题p成立时a的取值范围,再由二次函数的判别式求出命题q成立时a的取值范围,再求出p真q假和p假q真时a的取值范围,最后取并集即可.
解答:解:由题意易知:p:0<a<1,q:(2a-3)2-4>0,即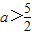 ,或
,或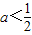 .
.
又因为p和q有且只有一个正确,
所以若p真q假,即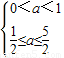 ,得
,得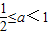 ;(4分)
;(4分)
若p假q真,即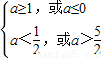 ,得a≤0,或
,得a≤0,或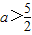 .(7分)
.(7分)
综上可得a的取值范围是a≤0, ≤a<1,或
≤a<1,或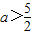 .(8分)
.(8分)
点评:本题考查了对数函数的单调性、二次函数根的判定及否命题的知识.
解答:解:由题意易知:p:0<a<1,q:(2a-3)2-4>0,即
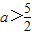 ,或
,或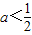 .
.又因为p和q有且只有一个正确,
所以若p真q假,即
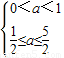 ,得
,得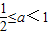 ;(4分)
;(4分)若p假q真,即
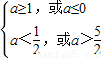 ,得a≤0,或
,得a≤0,或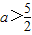 .(7分)
.(7分)综上可得a的取值范围是a≤0,
 ≤a<1,或
≤a<1,或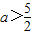 .(8分)
.(8分)点评:本题考查了对数函数的单调性、二次函数根的判定及否命题的知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. .
.