题目内容
(本小题满分13分)已知函数f(x)=x2+ax+b的两个零点是-2和3
(1)求a+b的值。 (2)求不等式af(-2x)>0的解集。
(1)求a+b的值。 (2)求不等式af(-2x)>0的解集。
(1)a+b=-7;
(2)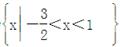
(2)
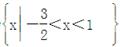
本试题主要是考查了函数的零点和不等是的 解集的问题的综合运用。
(1)利用函数f(x)=x2+ax+b的两个零点是-2,3.,从而说明-2,3是方程x2+ax+b=0的两根,然后李海勇韦达定理得到参数a,b的值。
(2)在第一问的基础上,不等式af(-2x)>0,即-(4x2+2x-6)>0?2x2+x-3<0可解得。
解:(1)∵f(x)=x2+ax+b的两个零点是-2,3.
∴-2,3是方程x2+ax+b=0的两根,---------2分
由根与系数的关系知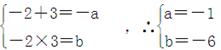 ,---------5分
,---------5分
∴a+b=-7---------6分
(2) ∵ f(x)=x2-x-6----------8分
∵不等式af(-2x)>0,
即-(4x2+2x-6)>0?2x2+x-3<0,----------10分
解集为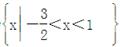 .---------13分
.---------13分
(1)利用函数f(x)=x2+ax+b的两个零点是-2,3.,从而说明-2,3是方程x2+ax+b=0的两根,然后李海勇韦达定理得到参数a,b的值。
(2)在第一问的基础上,不等式af(-2x)>0,即-(4x2+2x-6)>0?2x2+x-3<0可解得。
解:(1)∵f(x)=x2+ax+b的两个零点是-2,3.
∴-2,3是方程x2+ax+b=0的两根,---------2分
由根与系数的关系知
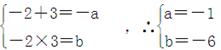 ,---------5分
,---------5分∴a+b=-7---------6分
(2) ∵ f(x)=x2-x-6----------8分
∵不等式af(-2x)>0,
即-(4x2+2x-6)>0?2x2+x-3<0,----------10分
解集为
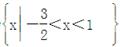 .---------13分
.---------13分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的零点所在的大致范围是( )
的零点所在的大致范围是( )



 ,若实数
,若实数 是方程
是方程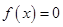 的解,且
的解,且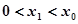 ,
,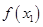 的值为( )
的值为( )
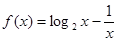 的零点所在的区间为( )
的零点所在的区间为( )


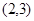
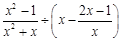 ,其中x是一元二次方程
,其中x是一元二次方程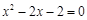 的正数根.
的正数根.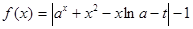
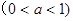 有零点,则实数
有零点,则实数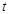 的最小值是
的最小值是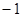
 ,则
,则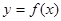
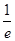 ,
,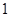 )、(
)、(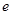 )内均有零点
)内均有零点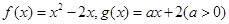 ,对任意
,对任意
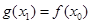 ,则
,则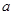 的取值范围是( )
的取值范围是( )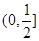
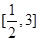
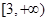

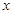 有
有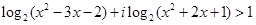 ,则
,则