题目内容
对任意一个非零复数z,定义集合 .
.(Ⅰ)设α是方程
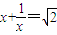 的一个根.试用列举法表示集合Ma,若在Ma中任取两个数,求其和为零的概率P;
的一个根.试用列举法表示集合Ma,若在Ma中任取两个数,求其和为零的概率P;(Ⅱ)设复数ω∈Mz,求证:Mω⊆Mz.
【答案】分析:(Ⅰ)由α是方程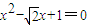 的根,可得
的根,可得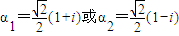 .当
.当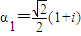 时,由
时,由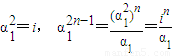 ,可得
,可得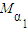 =
=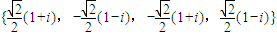 . 当
. 当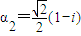 时,同理求得
时,同理求得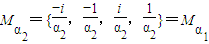 .由此求得在Ma中任取两个数,求其和为零的概率.
.由此求得在Ma中任取两个数,求其和为零的概率.
(Ⅱ)由ω∈Mz,可得存在m∈N,使得ω=z2m-1.于是对任意n∈N,ω2n-1=z(2m-1)(2n-1),由于(2m-1)(2n-1)是正奇数,ω2n-1∈Mz,命题得证.
解答:解:(Ⅰ)∵α是方程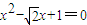 的根,∴
的根,∴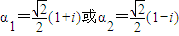 .…(2分)
.…(2分)
当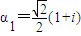 时,∵
时,∵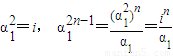 ,
,
∴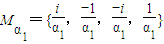 =
=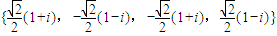 .
.
当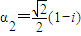 时,∵
时,∵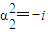 ,
,
∴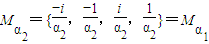 =
=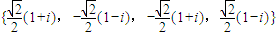 .
.
当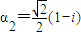 时,∵
时,∵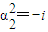 ,∴
,∴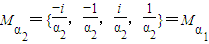 .
.
因此,不论α取哪一个值,集合Mα是不变的,即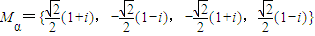 .…(8分)
.…(8分)
于是,在Ma中任取两个数,求其和为零的概率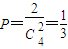 .…(10分)
.…(10分)
(Ⅱ)证明:∵ω∈Mz,∴存在m∈N,使得ω=z2m-1.…(12分)
于是对任意n∈N,ω2n-1=z(2m-1)(2n-1),由于(2m-1)(2n-1)是正奇数,ω2n-1∈Mz,所以Mω⊆Mz.…(14分)
点评:本题主要考查两个复数代数形式的混合运算,等可能事件的概率求法,体现了分类讨论的数学思想,属于中档题.
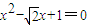 的根,可得
的根,可得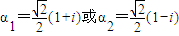 .当
.当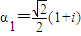 时,由
时,由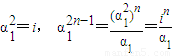 ,可得
,可得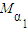 =
=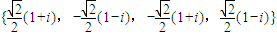 . 当
. 当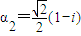 时,同理求得
时,同理求得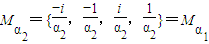 .由此求得在Ma中任取两个数,求其和为零的概率.
.由此求得在Ma中任取两个数,求其和为零的概率.(Ⅱ)由ω∈Mz,可得存在m∈N,使得ω=z2m-1.于是对任意n∈N,ω2n-1=z(2m-1)(2n-1),由于(2m-1)(2n-1)是正奇数,ω2n-1∈Mz,命题得证.
解答:解:(Ⅰ)∵α是方程
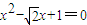 的根,∴
的根,∴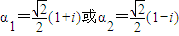 .…(2分)
.…(2分)当
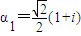 时,∵
时,∵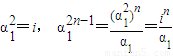 ,
,∴
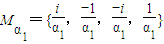 =
=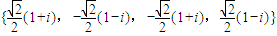 .
.当
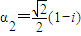 时,∵
时,∵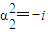 ,
,∴
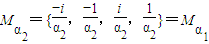 =
=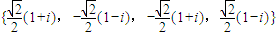 .
.当
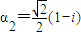 时,∵
时,∵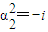 ,∴
,∴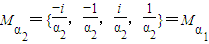 .
.因此,不论α取哪一个值,集合Mα是不变的,即
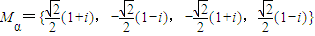 .…(8分)
.…(8分)于是,在Ma中任取两个数,求其和为零的概率
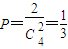 .…(10分)
.…(10分)(Ⅱ)证明:∵ω∈Mz,∴存在m∈N,使得ω=z2m-1.…(12分)
于是对任意n∈N,ω2n-1=z(2m-1)(2n-1),由于(2m-1)(2n-1)是正奇数,ω2n-1∈Mz,所以Mω⊆Mz.…(14分)
点评:本题主要考查两个复数代数形式的混合运算,等可能事件的概率求法,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目