题目内容
(2001•上海)对任意一个非零复数z,定义集合Mz={w|w=z2n-1,n∈N}.
(Ⅰ)设α是方程x+
=
的一个根.试用列举法表示集合Ma,若在Ma中任取两个数,求其和为零的概率P;
(Ⅱ)设复数ω∈Mz,求证:Mω⊆Mz.
(Ⅰ)设α是方程x+
| 1 |
| x |
| 2 |
(Ⅱ)设复数ω∈Mz,求证:Mω⊆Mz.
分析:(Ⅰ)由α是方程x2-
x+1=0的根,可得α1=
(1+i)或α2=
(1-i).当α1=
(1+i)时,由
=i,
=
=
,可得Mα1={
(1+i),-
(1-i),-
(1+i),
(1-i)}. 当α2=
(1-i)时,同理求得Mα2={
,
,
,
}=Mα1.由此求得在Ma中任取两个数,求其和为零的概率.
(Ⅱ)由ω∈Mz,可得存在m∈N,使得ω=z2m-1.于是对任意n∈N,ω2n-1=z(2m-1)(2n-1),由于(2m-1)(2n-1)是正奇数,ω2n-1∈Mz,命题得证.
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| α | 2 1 |
| α | 2n-1 1 |
(
| ||
| α1 |
| in |
| α1 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| -i |
| α2 |
| -1 |
| α2 |
| i |
| α2 |
| 1 |
| α2 |
(Ⅱ)由ω∈Mz,可得存在m∈N,使得ω=z2m-1.于是对任意n∈N,ω2n-1=z(2m-1)(2n-1),由于(2m-1)(2n-1)是正奇数,ω2n-1∈Mz,命题得证.
解答:解:(Ⅰ)∵α是方程x2-
x+1=0的根,∴α1=
(1+i)或α2=
(1-i).…(2分)
当α1=
(1+i)时,∵
=i,
=
=
,
∴Mα1={
,
,
,
}={
(1+i),-
(1-i),-
(1+i),
(1-i)}.
当α2=
(1-i)时,∵
=-i,
∴Mα2={
,
,
,
}=Mα1={
(1+i),-
(1-i),-
(1+i),
(1-i)}.
当α2=
(1-i)时,∵
=-i,∴Mα2={
,
,
,
}=Mα1.
因此,不论α取哪一个值,集合Mα是不变的,即Mα={
(1+i),-
(1-i),-
(1+i),
(1-i)}.…(8分)
于是,在Ma中任取两个数,求其和为零的概率 P=
=
.…(10分)
(Ⅱ)证明:∵ω∈Mz,∴存在m∈N,使得ω=z2m-1.…(12分)
于是对任意n∈N,ω2n-1=z(2m-1)(2n-1),由于(2m-1)(2n-1)是正奇数,ω2n-1∈Mz,所以Mω⊆Mz.…(14分)
| 2 |
| ||
| 2 |
| ||
| 2 |
当α1=
| ||
| 2 |
| α | 2 1 |
| α | 2n-1 1 |
(
| ||
| α1 |
| in |
| α1 |
∴Mα1={
| i |
| α1 |
| -1 |
| α1 |
| -i |
| α1 |
| 1 |
| α1 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
当α2=
| ||
| 2 |
| α | 2 2 |
∴Mα2={
| -i |
| α2 |
| -1 |
| α2 |
| i |
| α2 |
| 1 |
| α2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
当α2=
| ||
| 2 |
| α | 2 2 |
| -i |
| α2 |
| -1 |
| α2 |
| i |
| α2 |
| 1 |
| α2 |
因此,不论α取哪一个值,集合Mα是不变的,即Mα={
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
于是,在Ma中任取两个数,求其和为零的概率 P=
| 2 | ||
|
| 1 |
| 3 |
(Ⅱ)证明:∵ω∈Mz,∴存在m∈N,使得ω=z2m-1.…(12分)
于是对任意n∈N,ω2n-1=z(2m-1)(2n-1),由于(2m-1)(2n-1)是正奇数,ω2n-1∈Mz,所以Mω⊆Mz.…(14分)
点评:本题主要考查两个复数代数形式的混合运算,等可能事件的概率求法,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
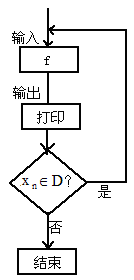
 (2001•上海)对任意函数f(x),x∈D,可按图示构造一个数列发生器,其工作原理如下:
(2001•上海)对任意函数f(x),x∈D,可按图示构造一个数列发生器,其工作原理如下: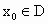 ,经数列发生器输出
,经数列发生器输出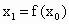 ;②若
;②若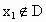 ,则数列发生器结束工作;若
,则数列发生器结束工作;若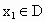 ,将
,将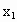 反馈回输入端,再输出
反馈回输入端,再输出 ,并依此规律进行下去.现定义
,并依此规律进行下去.现定义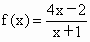 .
.
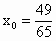 ,则由数列发生器产生数列
,则由数列发生器产生数列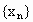 ,写出数列
,写出数列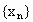 的所有项;
的所有项;
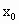 的值.
的值.