题目内容
已知数列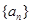 满足
满足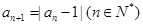 ,
,
(1)若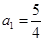 ,求
,求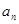 ;
;
(2)是否存在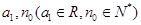 ,使当
,使当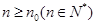 时,
时,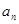 恒为常数.若存在求
恒为常数.若存在求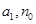 ,否则说明理由;
,否则说明理由;
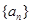 满足
满足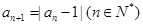 ,
,(1)若
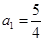 ,求
,求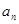 ;
;(2)是否存在
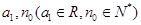 ,使当
,使当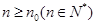 时,
时,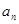 恒为常数.若存在求
恒为常数.若存在求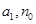 ,否则说明理由;
,否则说明理由;(1)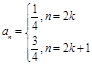 其中
其中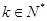
(2)存在三组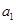 和
和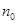 :
:
 时,
时, ;
; 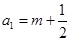 时,
时, ;
; 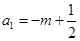 时,
时, 其中
其中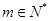
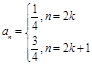 其中
其中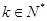
(2)存在三组
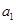 和
和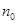 :
: 时,
时, ;
; 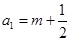 时,
时, ;
; 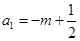 时,
时, 其中
其中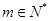
(1)根据递推关系可由a1,分别求出a2,a3,a4,然后归纳出an的通项公式.
(2)本小题难度偏大,应从特值出发探索,做此类问题应有较强的计算能力,逻辑分析能力,和扎实的数学基本功,还要有坚强的意志.
解:(1)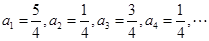 2分
2分
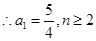 时,
时,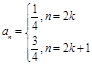 ,其中
,其中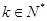 ` ………….6分
` ………….6分
(2)因为存在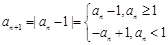 ,所以当
,所以当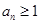 时,
时,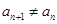
①若 ,则
,则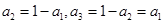 ,此时只需:
,此时只需:
故存在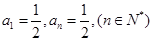 ……………..8分
……………..8分
②若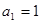 不符合题意………………9分
不符合题意………………9分
③若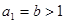 ,不妨设
,不妨设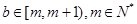 ,易知
,易知 ,
,
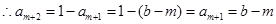
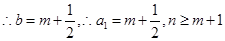 时,
时,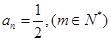 …………….11分
…………….11分
④若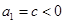 ,不妨设
,不妨设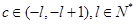 ,易知
,易知
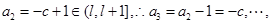
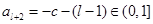
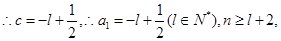 则
则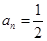 ………..13分
………..13分
故存在三组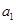 和
和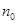 :
:
 时,
时, ;
; 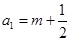 时,
时, ;
; 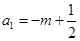 时,
时, 其中
其中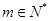 …………14分
…………14分
(2)本小题难度偏大,应从特值出发探索,做此类问题应有较强的计算能力,逻辑分析能力,和扎实的数学基本功,还要有坚强的意志.
解:(1)
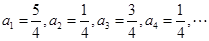 2分
2分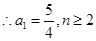 时,
时,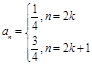 ,其中
,其中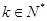 ` ………….6分
` ………….6分(2)因为存在
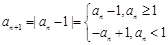 ,所以当
,所以当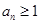 时,
时,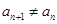
①若
 ,则
,则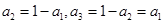 ,此时只需:
,此时只需:
故存在
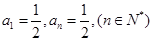 ……………..8分
……………..8分 ②若
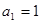 不符合题意………………9分
不符合题意………………9分③若
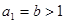 ,不妨设
,不妨设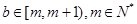 ,易知
,易知 ,
, 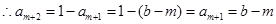
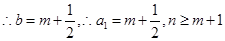 时,
时,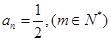 …………….11分
…………….11分④若
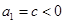 ,不妨设
,不妨设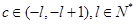 ,易知
,易知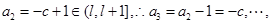
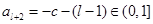
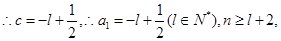 则
则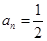 ………..13分
………..13分 故存在三组
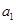 和
和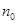 :
: 时,
时, ;
; 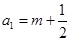 时,
时, ;
; 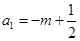 时,
时, 其中
其中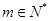 …………14分
…………14分
练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
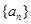 的前
的前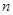 项和为
项和为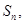 已知
已知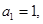
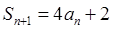
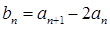 ,证明数列
,证明数列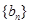 是等比数列;
是等比数列; 
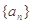 是等比数列,且公比
是等比数列,且公比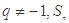 是
是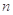 项和,已知
项和,已知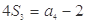 ,
,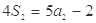 ,则公比
,则公比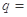 ( )
( )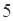



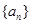 的前
的前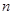 项和记为
项和记为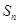 ,若
,若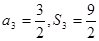 ,求求通项
,求求通项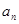 .
.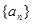 是公比为
是公比为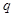 的等比数列,首项
的等比数列,首项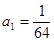 ,
,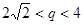 ,对于
,对于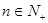 ,
,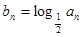 ,若数列
,若数列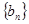 的前
的前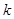 项和取得最大值,则
项和取得最大值,则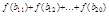 =
= 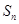 为等比数列
为等比数列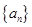 的前
的前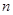 项和,已知
项和,已知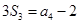 ,
,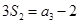 ,则公比
,则公比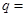 ( )
( )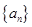 中,
中,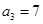 ,前3项之和
,前3项之和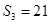 ,则公比
,则公比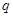 的值为 ( )
的值为 ( )
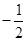
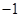 或
或
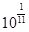 ,
,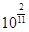 ,
,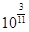 ,…,
,…,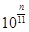 ,…,使数列前n项的乘积不超过
,…,使数列前n项的乘积不超过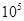 的最大正整数n是 ( )
的最大正整数n是 ( )