题目内容
若对于预报变量y与解释变量x的10组统计数据的回归模型中,计算R2=0.95,又知残差平方和为120.55,那么 的值为( )
的值为( )
| A.241.1 | B.245.1 | C.2411 | D.2451 |
C.
解析试题分析:设 ,根据条件残差平方和为
,根据条件残差平方和为 ,即
,即 由公式
由公式 ,可得
,可得 .
.
考点:残差平方和,总偏差平方和和相关指数的关系.

练习册系列答案
相关题目
某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本.若样本中的青年职工为7人,则样本容量为( )
| A.7 | B.25 | C.15 | D.35 |
已知某地区中小学生人数和近视情况分别如图1和如图2所示,为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取 的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )
的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )

A. , , | B. , , | C. , , | D. , , |
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据 (
( =1,2, ,n),用最小二乘法建立的回归方程为
=1,2, ,n),用最小二乘法建立的回归方程为 =0.85x-85.71,则下列结论中不正确的是( )
=0.85x-85.71,则下列结论中不正确的是( )
| A.y与x具有正的线性相关关系 |
B.回归直线过样本点的中心 |
| C.若该大学某女生身高增加1cm,则其体重约增加0.85kg |
| D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg |
由于工业化城镇化的推进,大气污染日益加重,空气质量逐步恶化,雾霾天气频率增大,大气污染可引起心悸、胸闷等心脏病症状.为了解某市患心脏病是否与性别有关,在某医院心血管科随机的对入院50位进行调查得到了如下列联表:问有多大的把握认为是否患心脏病与性别有关. 答:.
| A.95% | B.99% | C.99.5% | D.99.9% |
| | 患心脏病 | 不患心脏病 | 合计 |
| 男 | 20 | 5 | 25 |
| 女 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
参考临界值表:
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 其中n =" a" + b + c + d).
其中n =" a" + b + c + d). 如果一组数中每个数减去同一个非零常数,则这一组数的( )
| A.平均数不变,方差不变 | B.平均数改变,方差改变 |
| C.平均数不变,方差改变 | D.平均数改变,方差不变 |
 位员工的月工资(单位:元)为
位员工的月工资(单位:元)为 ,
, ,…,
,…, ,其均值和方差分别为
,其均值和方差分别为 和
和 ,若从下月起每位员工的月工资增加
,若从下月起每位员工的月工资增加 元,则这
元,则这
 ,
,

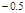
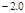

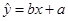 ,则( )
,则( ) ,
, B.
B.
 ,
,