题目内容

下列命题中正确的有

①若向量a与b满足a·b＜0，则a与b所成角为钝角

②若向量a与b不共线，m=λ1a+λ2b,n=μ1a+μ2b,(λ1,λ2,μ1,μ2∈R),则m∥n的充要条件是λ1μ2-λ2·μ1=0

③若++=0,且||=||=||，则△ABC是等边三角形

④若a与b为非零向量，且a⊥b,则|a+b|=|a-b|

A.②③④             B.①②③             C.①④              D.②

A

解析:①中若=-1,则a与b所成的角为180°，故①错；

②中若m∥n,则m=kn,即(λ1a+λ2b)=k(μ1a+μ2b),可得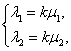消k得λ1μ2-λ2μ1=0,故②正确；③中由条件可得∠AOB=∠BOC=∠AOC=120°,且||=||=||,故AB=AC=BC，∴③正确；④中由a⊥b得a·b=0,故|a+b|2=a2+b2+2a·b=a2+b2,|a-b|2=a2+b2-2a·b=a2+b2,

∴|a+b|=|a-b|，故④正确.∴选A.

练习册系列答案
相关题目
下列命题中正确的有
 
．（填写所有正确命题的序号）
①在△ABC中，若A＞B，则sinA＞sinB；
②若△ABC为锐角三角形，则sinA＞cosB；
③若数列{an}为等差数列，则数列an+2an+1仍为等差数列；
④若数列{an}为等比数列，则数列an+2an+1仍为等比数列；
⑤当x∈(0，
π
2
]时，y=sinx+
2
sinx
的最小值是2
2
．
下列命题中正确的有
 
．（填上所有正确命题的序号）
①若f（x）可导且f'（x0）=0，则x0是f（x）的极值点；
②函数f（x）=xe-x，x∈[2，4]的最大值为2e-2；
③已知函数f(x)=
-x2+2x
，则∫_1f(x)dx的值为
π
4
；
④一质点在直线上以速度v=t2-4t+3（m/s）运动，从时刻t=0（s）到t=4（s）时质点运动的路程为
4
3
(m)．
已知m、n为两条不同直线，α、β为两个不重合的平面，给出下列命题中正确的有（　　）
①
m⊥α
m⊥n
⇒n∥α；
②
m⊥β
n⊥β
⇒m∥n；
③
m⊥α
m⊥β
⇒α∥β；
④
m?α
n?α
α∥β
⇒m∥n．
下列命题中正确的有
（3）（5）
（3）（5）
（填正确命题的序号）．
（1）空集是任意集合的真子集；
（2）若f（1）+f（-1）=0，则函数f（x）是奇函数；
（3）函数y=(
1
2
)-x 的反函数为y=log2x；
（4）函数y=f（x）是区间（a，b）上的增函数，则函数y=2012f（x）-
2012
f(x)
也是区间（a，b） 上的增函数；
（5）若函数f （x）满足f（-x）=f（x），且当x∈[0，+∞）时f（x）=x2+2x-2，则关于x不等式f（x-1）＜1的解集为（0，2）．
下列命题中正确的有
③④
③④
．（填上所有正确命题的序号）
①若f'（x0）=0，则函数y=f（x）在x=x0取得极值；
②若∫abf（x）dx＞0，则f（x）＞0在[a，b]上恒成立；
③已知函数f（x）=
-x2+2x
，则∫01f（x）dx的值为
π
4
；
④一质点在直线上以速度v=t2-4t+3（m/s）运动，从时刻t=0（s）到t=4（s）时质点运动的位移为
4
3
（m）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网