题目内容
选修4-4:极坐标与参数方程
在直角坐标系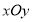 中,曲线
中,曲线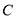 的参数方程为
的参数方程为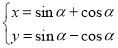 (
(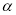 为参数)
为参数)
(1)求曲线 的普通方程;
的普通方程;
(2)在以 为极点,
为极点,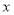 正半轴为极轴的极坐标系中,直线
正半轴为极轴的极坐标系中,直线 方程为
方程为 ,
,
已知直线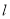 与曲线
与曲线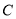 相交于
相交于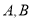 两点,求
两点,求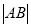 .
.
练习册系列答案
相关题目
已知定义在R上的函数f(x)的图像是连续不断的,且有如下对应值表:
x | 0 | 1 | 2 | 3 |
f(x) | 3.1 | 0.1 | -0.9 | -3 |
那么函数f(x)一定存在零点的区间是 ( )
A.(0,1) B.(1,2) C.(2,3) D.(3,+∞)


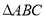 的三边长为
的三边长为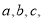 满足直线
满足直线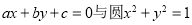 相离,则
相离,则
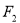 是椭圆 C:
是椭圆 C: (
( >b>0)的两个焦点,P为椭圆 C上一点,且
>b>0)的两个焦点,P为椭圆 C上一点,且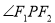 =
= ,若
,若 的面积为
的面积为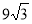 ,则b=( )
,则b=( ) 为两个定点,
为两个定点,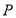 为动点,若
为动点,若 ,则动点P的轨迹为( )
,则动点P的轨迹为( ) 单调递增,记数列
单调递增,记数列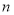 项之和为
项之和为 ,且满足条件
,且满足条件
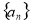 的通项公式;
的通项公式;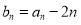 ,求数列
,求数列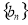 的前
的前 项之和
项之和 .
. 满足条件
满足条件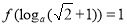 ,其中
,其中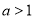 ,则
,则 ( )
( )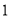 B.
B.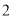 C.
C.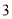 D.
D.
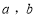 满足
满足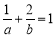 ,则
,则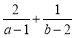 的最小值为 .
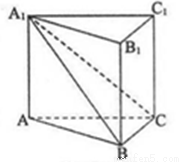
的最小值为 .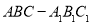 中,平面
中,平面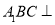 侧面
侧面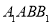 ,且
,且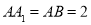 .
.
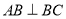 ;
;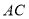 与平面
与平面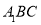 所成角的大小为
所成角的大小为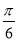 ,求锐二面角
,求锐二面角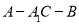 的大小.
的大小.