题目内容
求证:(1)若f(x)可导且为偶函数,则f′(x)为奇函数;(2)若f(x)可导且为奇函数,则f′(x)为偶函数.
思路分析:只需证明f′(-x)=-f′(x)或f′(-x)=f′(x)即可.
解:(1)依题意,设x是定义域内的任一实数,则f(-x)=f(x),两边对x求导得f′(-x)(-x)′=f′(x),即f′(-x)=
-f′(x).∴f′(x)是奇函数.
(2)依题意,设x是定义域内的任一实数,则f(-x)=-f(x),两边对x求导得-f′(-x)=-f′(x).
∴f′(-x)=f′(x),f′(x)是偶函数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
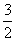 ,求实数a的值;
,求实数a的值;