题目内容

已知P={
a
|
a
=（1，0）+m（0，1），m∈R}，Q={
b
|
b
=（1，1）+n（-1，1），n∈R}是两个向量集合，则P∩Q=（　　）
A、{（1，1）}
B、{（-1，1）}
C、{（1，0）}
D、{（0，1）}
分析：先根据向量的线性运算化简集合P，Q，求集合的交集就是寻找这两个集合的公共元素，通过列方程组解得．
解答：解：由已知可求得P={（1，m）}，Q={（1-n，1+n）}，
再由交集的含义，有
1=1-n
m=1+n
?
n=0
m=1
，
所以选A．
点评：本题主要考查交集及其运算，属于基础题．
练习册系列答案
相关题目
已知p：A={x||x-a|＜4}；q：{x|（x-2）（3-x）＞0}，且非p是非q的充分条件，则a的取值范围为（　　）
A、-1＜a＜6B、-1≤a≤6C、a＜-1或a＞6D、a≤-1或a≥6
已知P={
a
|
a
=（1，0）+m（0，1），m∈R}，Q={
b
|
b
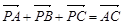=（1，1）+n（-1，1），n∈R}是两个向量集合，则P∩Q=
{（1，1）}
{（1，1）}
．
已知p=a+(a＞2),q=(a＞2),则(    )

A.p＞q                B.p＜q                  C.p≥q                 D.p≤q

已知P,A,B,C是平面内四个不同的点，且，则(    )

A.  A,B,C三点共线            B.  A,B,P三点共线   

C.  A,C,P三点共线            D.  B,C,P三点共线

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网