题目内容
经过点(2,1)的直线l到A(1,1),B(3,5)两点的距离相等,则直线l的方程为( )
| A、2x-y-3=0 | B、x=2 | C、2x-y-3=0或x=2 | D、都不对 |
分析:分两种情况考虑,当直线l的斜率不存在时,得到直线x=2显然满足题意;当直线l的斜率存在时,设出直线l的斜率为k,根据已知点的坐标表示出直线l的方程,然后利用点到直线的距离公式表示出A到直线l的距离和B到直线l的距离,让两距离相等即可得到关于k的方程,求出方程的解即可得到k的值,写出直线l的方程即可,综上,得到所有满足题意的直线l的方程.
解答:解:当直线l的斜率不存在时,直线x=2显然满足题意;
当直线l的斜率垂存在时,设直线l的斜率为k,
则直线l为y-1=k(x-2),即kx-y+1-2k=0,
由A到直线l的距离等于B到直线l的距离得:
=
,化简得:-k=k-4或k=k-4(无解),解得k=2,
所以直线l的方程为2x-y-3=0,
综上,直线l的方程为2x-y-3=0或x=2.
故选C
当直线l的斜率垂存在时,设直线l的斜率为k,
则直线l为y-1=k(x-2),即kx-y+1-2k=0,
由A到直线l的距离等于B到直线l的距离得:
| |-k| | ||
|
| |k-4| | ||
|
所以直线l的方程为2x-y-3=0,
综上,直线l的方程为2x-y-3=0或x=2.
故选C
点评:此题考查学生灵活运用点到直线的距离公式化简求值,是一道基础题.学生做题是容易把斜率不存在的情况遗漏,做题时应注意这点.

练习册系列答案
相关题目
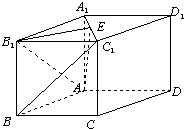 如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为a的菱形,且∠ABC=60°,侧棱长为
如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为a的菱形,且∠ABC=60°,侧棱长为 开始依次水平向右和竖直向上跳动,其落点坐标依次是
开始依次水平向右和竖直向上跳动,其落点坐标依次是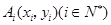 ,(如图所示,
,(如图所示, 坐标以已知条件为准),
坐标以已知条件为准), 表示青蛙从点
表示青蛙从点 到点
到点 所经过的路程。
所经过的路程。
 准线上
准线上 ,
, 均在该抛物线上,并且直线
均在该抛物线上,并且直线 .
.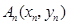 要么落在
要么落在 所表示的曲线上,
所表示的曲线上, 所表示的曲线上,并且
所表示的曲线上,并且 ,
, (不需证明);
(不需证明); 所表示的曲线上,要么落在
所表示的曲线上,要么落在 所表示的曲线上,并且
所表示的曲线上,并且 ,求
,求
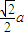 ,若经过AB1且与BC1平行的平面交上底面线段A1C1于点E.
,若经过AB1且与BC1平行的平面交上底面线段A1C1于点E.