Question

（Ⅰ）已知函数f(x)=x²+lnx-ax在(0,1)上是增函数，求a的取值范围.

（Ⅱ）在（Ⅰ）的结论下，设g(x)=e²x+|e^x-a|,x∈［0,ln3］.求函数g(x)的最小值.

Answer 1

解：f′(x)=,∵f(x)在(0,1)上增，

∴f′(x)≥0在（0，1）上恒成立，

∴2x²-ax+1≥0,∴a≤=+2x.

∵+2x≥2,∴a≤2.

(Ⅱ)∵x∈［0,ln3］,

∴e^x∈［1,3］.

    当a≤1时，g(x)=e²x+e^x-a.此时，g(x)在x∈［0,ln3］上增，∴g(x)_min=2-a;

    当1＜a≤22时，g(x)=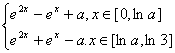

    当x∈［0,lna］时，g′(x)=2e²x-e^x＞0.

    此时g(x)最小值g(0)=a;

    当x∈［lna,ln3］时，g(x)单调递增，

g(x)最小值为g(lna)=(e^lna)²=a²;

∵a＜a²,

    故g(x)_min=a.

    综上：a≤1时，g(x)_min=2-a;

1＜a≤2时，g(x)_min=a.