题目内容
已知数列![]() 单调递增,且各项非负.对于正整数
单调递增,且各项非负.对于正整数![]() ,若任意的
,若任意的![]() ,
,![]() 仍是
仍是![]() 中的项,则称数列
中的项,则称数列![]() 为“
为“![]() 项可减数列”.
项可减数列”.
(Ⅰ)已知数列![]() 是首项为2,公比为2的等比数列,且数列
是首项为2,公比为2的等比数列,且数列![]() 是“
是“![]() 项可减数列”,试确定
项可减数列”,试确定![]() 的最大值.
的最大值.
(Ⅱ)求证:若数列![]() 是“
是“![]() 项可减数列”,则其前
项可减数列”,则其前![]() 项的和
项的和![]() .
.
(Ⅲ)已知![]() 是各项非负的递增数列,写出(Ⅱ)的逆命题,判断该逆命题的真假,并说明理由.
是各项非负的递增数列,写出(Ⅱ)的逆命题,判断该逆命题的真假,并说明理由.
(Ⅰ) 解:设![]() ,则
,则![]() ,
,
易得![]() , 即数列
, 即数列![]() 一定是“2项可减数列” …………………2分
一定是“2项可减数列” …………………2分
但因为![]() ,所以
,所以![]() 的最大值为2……………………………………4分
的最大值为2……………………………………4分
(Ⅱ)证明:因为数列![]() 是“
是“![]() 项可减数列”,所以
项可减数列”,所以![]() 必定是数列
必定是数列![]() 中的项,
中的项,
而![]() 是递增数列,
是递增数列,![]() ,
,
所以必有![]() ………………………………6分
………………………………6分
故![]()
![]() , 所以
, 所以![]() ,即
,即![]() ……………………………8分
……………………………8分
又由定义知,数列![]() 也是“t项可减数列”(
也是“t项可减数列”(![]() ),
),
所以![]() …………………………………………………………………………… 9分
…………………………………………………………………………… 9分
(Ⅲ)解:(Ⅱ)的逆命题为:已知数列![]() 为各项非负的递增数列,若其前
为各项非负的递增数列,若其前![]() 项的和满足
项的和满足
![]() ,则该数列一定是“
,则该数列一定是“![]() 项可减数列” ………………………………………10分
项可减数列” ………………………………………10分
该逆命题为真命题…………………………………………………………………………………………11分
理由如下:因为![]() ,所以当
,所以当![]() 时,
时,![]() ,两式相减,
,两式相减,
得![]() ,即
,即![]() (*) …………………………12分
(*) …………………………12分
则当![]() 时,有
时,有![]() (**),由(**)-(*),得
(**),由(**)-(*),得![]() ……………13分
……………13分
又![]() ,所以
,所以![]() ,故数列
,故数列![]() 是首项为0的递增等差数列………………………… 14分
是首项为0的递增等差数列………………………… 14分
设公差为![]() ,则
,则![]()
对于任意的![]() ,
,![]() ……………………………………………15分
……………………………………………15分
因为![]() ,所以
,所以![]() 仍是
仍是![]() 中的项,故数列
中的项,故数列![]() 是“
是“![]() 项可减数列”……16分
项可减数列”……16分

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
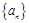 单调递增,且各项非负,对于正整数
单调递增,且各项非负,对于正整数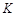 ,若任意的
,若任意的 ,
,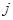 (
(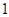 ≤
≤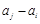 仍是
仍是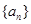 为“
为“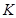 项可减数列”.
项可减数列”.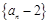 是“
是“ 项的和
项的和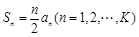 ;
;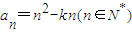 ,且{an}单调递增,则k的取值范围是( )
,且{an}单调递增,则k的取值范围是( )