题目内容
在下列五个命题中,①函数y=sin(
| 5π |
| 2 |
②已知cosα=
| 1 |
| 2 |
| π |
| 3 |
③直线x=
| π |
| 8 |
| 5π |
| 4 |
④△ABC中,若cosA>cosB,则A<B; ⑤函数y=|cos2x+
| 1 |
| 2 |
| π |
| 2 |
把你认为正确的命题的序号都填在横线上
分析:①函数y=sin(
-2x)=cos2x,所以函数是偶函数.
②由题意可得:α的取值集合是{
,-
};
③当x=
时,y=-1,进而得到直线时函数的对称轴.
④∵A∈(0,π),B∈(0,π),并且在(0,π)上,y=cosx是减函数进而得到答案.
⑤由函数y=|cos2x+
|的图象可得函数的周期是π;
| 5π |
| 2 |
②由题意可得:α的取值集合是{
| π |
| 3 |
| π |
| 3 |
③当x=
| π |
| 8 |
④∵A∈(0,π),B∈(0,π),并且在(0,π)上,y=cosx是减函数进而得到答案.
⑤由函数y=|cos2x+
| 1 |
| 2 |
解答:解:①函数y=sin(
-2x)=cos2x,所以函数是偶函数,所以①正确.
②已知cosα=
,且α∈[0,2π],则α的取值集合是{
,-
};所以②错误.
③当x=
时,y=sin(2x+
)=sin
=-1,所以③正确.
④∵A、B是三角形的内角,∴A∈(0,π),B∈(0,π),∵在(0,π)上,y=cosx是减函数,∴△ABC中,若cosA>cosB,则A<B.所以④正确.
⑤由函数y=|cos2x+
|的图象可得函数的周期是π;所以⑤错误.
故答案为①③④.
| 5π |
| 2 |
②已知cosα=
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
③当x=
| π |
| 8 |
| 5π |
| 4 |
| 3π |
| 2 |
④∵A、B是三角形的内角,∴A∈(0,π),B∈(0,π),∵在(0,π)上,y=cosx是减函数,∴△ABC中,若cosA>cosB,则A<B.所以④正确.
⑤由函数y=|cos2x+
| 1 |
| 2 |
故答案为①③④.
点评:解决此类问题的关键是熟练掌握三角函数的性质,以及诱导公式与有关公式.

练习册系列答案
相关题目
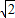 ,则a⊆{x}x>2
,则a⊆{x}x>2 };
};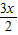 不是从P到Q的映射;
不是从P到Q的映射;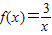 在(-∞,0)∪(0,+∞)上为减函数;
在(-∞,0)∪(0,+∞)上为减函数;