题目内容
在下列五个命题中：
①若a=3
，则a⊆{x}x＞2
}；
②若P={x|0≤x≤4}，Q={ y|0≤y≤2}，则对应y=
不是从P到Q的映射；
③f(x)=
在（-∞，0）∪（0，+∞）上为减函数；
④若函数y=f（x-1）的图象经过点（4，1），则函数y=f-1（x）的图象必经过点（1，3）；
⑤命题“对任意的x∈R，x3-x2+1≤0”的否定是“不存在x∈R，x3-x2+1≤0”．
其中所有不正确的命题的序号为
①若a=3
| 2 |
| 3 |
②若P={x|0≤x≤4}，Q={ y|0≤y≤2}，则对应y=
| 3x |
| 2 |
③f(x)=
| 3 |
| x |
④若函数y=f（x-1）的图象经过点（4，1），则函数y=f-1（x）的图象必经过点（1，3）；
⑤命题“对任意的x∈R，x3-x2+1≤0”的否定是“不存在x∈R，x3-x2+1≤0”．
其中所有不正确的命题的序号为
①③⑤
①③⑤
．分析：本题考查的知识点是，判断命题真假，可以运用函数反函数的知识，元素与集合的关系，全称命题的否定对四个结论逐一进行判断，可以得到正确的结论．
解答：解：①元素与集合的关系符号为∈或∉． 不为⊆，故①错．
②对于P中x=4，按照对应y=
，y=6，但6∉Q，即是说P存在元素没有像，不符合映射的概念． 故对．
③取两个自变量的值，-1，1，满足-1＜1，但f（-1）＜f（1），所以f(x)=
在（-∞，0）∪（0，+∞）上不为减函数；故错．
④若函数y=f（x-1）的图象经过点（4，1），则有f（3）=1，根据反函数概念得出1=f-1（3），即函数y=f-1（x）的图象必经过点（1，3）；④对．
⑤命题“对任意的x∈R，x3-x2+1≤0”的否定是“存在x∈R，x3-x2+1＞0”． 故错．
综上所述所有不正确的命题的序号为 ①③⑤
故答案为：①③⑤．
②对于P中x=4，按照对应y=
| 3x |
| 2 |
③取两个自变量的值，-1，1，满足-1＜1，但f（-1）＜f（1），所以f(x)=
| 3 |
| x |
④若函数y=f（x-1）的图象经过点（4，1），则有f（3）=1，根据反函数概念得出1=f-1（3），即函数y=f-1（x）的图象必经过点（1，3）；④对．
⑤命题“对任意的x∈R，x3-x2+1≤0”的否定是“存在x∈R，x3-x2+1＞0”． 故错．
综上所述所有不正确的命题的序号为 ①③⑤
故答案为：①③⑤．
点评：本题考查命题真假的判断．用到了集合、映射、函数单调性、反函数、全称命题的知识．是好题．
练习册系列答案
相关题目
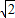，则a⊆{x}x＞2
}；
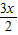不是从P到Q的映射；
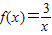在（-∞，0）∪（0，+∞）上为减函数；