题目内容
对称轴为坐标轴,顶点在坐标原点的抛物线C经过两点A(a,2a)、B(4a,4a)(其中a为正常数),
(1)求抛物线C的方程;
(2)设动点T(m,0)(m>a),直线AT、BT与抛物线C的另一个交点分别为A1、B1,当m变化时,记所有直线A1B1组成的集合为M,求证:集合M中的任意两条直线都相交且交点都不在坐标轴上。
(1)求抛物线C的方程;
(2)设动点T(m,0)(m>a),直线AT、BT与抛物线C的另一个交点分别为A1、B1,当m变化时,记所有直线A1B1组成的集合为M,求证:集合M中的任意两条直线都相交且交点都不在坐标轴上。
解:(1)当抛物线焦点在x轴上时,设抛物线方程y2=2px,
∵ ,
,
∴p=2a,
∴y2=4ax;
当抛物线焦点在y轴上时,设抛物线方程x2=2py,
∵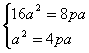 ,
,
∴方程无解,
∴抛物线不存在。
(2)设A1(as2,2as)、B1(at2,2at),T(m,0)(m>a),
∵ ,
,
∴ ,
,
∴as2+(m-a)s-m=0,
∵(as+m)(s-1)=0,
∴ ,
,
∴A1(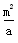 ,-2m),
,-2m),
∵ ,
,
∴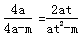 ,
,
∵2at2+(m-4a)t-2m=0,
∴(2at+m)(t-2)=0,
∴t=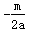 ,
,
∴B1(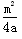 ,-m),
,-m),
∴ 的直线方程为y+2m=
的直线方程为y+2m=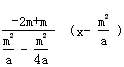 ,
,
∵直线的斜率为 在(a,+∞)单调,
在(a,+∞)单调,
∴所以集合M中的直线必定相交,
∵直线的横截距为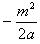 在(a,+∞)单调,纵截距为
在(a,+∞)单调,纵截距为 在(a,+∞)单调,
在(a,+∞)单调,
∴任意两条直线都相交且交点都不在坐标轴上。
∵
 ,
,∴p=2a,
∴y2=4ax;
当抛物线焦点在y轴上时,设抛物线方程x2=2py,
∵
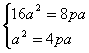 ,
,∴方程无解,
∴抛物线不存在。
(2)设A1(as2,2as)、B1(at2,2at),T(m,0)(m>a),
∵
 ,
,∴
 ,
,∴as2+(m-a)s-m=0,
∵(as+m)(s-1)=0,
∴
 ,
,∴A1(
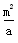 ,-2m),
,-2m),∵
 ,
,∴
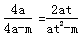 ,
,∵2at2+(m-4a)t-2m=0,
∴(2at+m)(t-2)=0,
∴t=
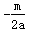 ,
,∴B1(
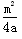 ,-m),
,-m),∴
 的直线方程为y+2m=
的直线方程为y+2m=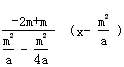 ,
,∵直线的斜率为
 在(a,+∞)单调,
在(a,+∞)单调,∴所以集合M中的直线必定相交,
∵直线的横截距为
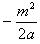 在(a,+∞)单调,纵截距为
在(a,+∞)单调,纵截距为 在(a,+∞)单调,
在(a,+∞)单调,∴任意两条直线都相交且交点都不在坐标轴上。

练习册系列答案
相关题目