��Ŀ����
ƽ��ֱ������ϵxOy�У���֪��M������F1��0��-c����F2��0��c����A��| 3 |
��1�����M�ı����̣��ú�c��ʽ�ӱ�ʾ����
��2����֪��Բ
| y2 |
| a2 |
| x2 |
| b2 |
������Բ�����ʵ�ȡֵ��Χ��
����A��B��M��O��C��D��OΪ����ԭ�㣩���ξ��ȷֲ���x���ϣ���ֱ��MF1��ֱ��DF2�Ľ����Ƿ���һ����ֱ���ϣ����ǣ������������ֱ�ߵķ��̣������ǣ���˵�����ɣ�
��������1�����M�ķ���Ϊx2+y2+Dx+Ey+F=0���������裬��
���ɴ��������M�ķ��̣�
��2����M��x�����������A(
c��0)��C(-
c��0)����B��b��0����D��-b��0����������
���ɴ��������Բ�����ʵ�ȡֵ��Χ��
��3����M(
c��0)����
c-b=b-
c=
c������ֱ��MF1�ķ���Ϊ
-
=1���ɴ��ܹ�����ֱ��MF1��ֱ��DF2�Ľ���Q�ڶ�ֱ��y=
x�ϣ�
|
��2����M��x�����������A(
| 3 |
| ||
| 3 |
|
��3����M(
| ||
| 3 |
| 3 |
| ||
| 3 |
| ||
| 3 |
| x | ||||
|
| y |
| c |
3
| ||
| 4 |
����⣺��1�����M�ķ���Ϊx2+y2+Dx+Ey+F=0��
�������裬��
���
��M�ķ���Ϊx2+y2-
cx-c2=0��
��M�ı�����Ϊ(x-
c)2+y2=
c2����5�֣�
��2����M��x�����������A(
c��0)��C(-
c��0)��
��B��b��0����D��-b��0����
������
��
����
���
��
��
��
��
��e��
��������Բ�����ʵ�ȡֵ��ΧΪ(
��
)����10�֣�
��3���ɣ�1������M(
c��0)��
�����裬��
c-b=b-
c=
c��
��b=
c��D(-
c��0)��
��ֱ��MF1�ķ���Ϊ
-
=1��
��ֱ��DF2�ķ���Ϊ-
+
=1��
���ɢ٢ڣ���ֱ��MF1��ֱ��DF2�Ľ���Q(
c��3c)��
��֪kOQ=
Ϊ��ֵ��
��ֱ��MF1��ֱ��DF2�Ľ���Q�ڶ�ֱ��y=
x�ϣ���15�֣�
�������裬��
|
���
|
��M�ķ���Ϊx2+y2-
2
| ||
| 3 |
��M�ı�����Ϊ(x-
| ||
| 3 |
| 4 |
| 3 |
��2����M��x�����������A(
| 3 |
| ||
| 3 |
��B��b��0����D��-b��0����
������
|
|
����
|
| 1 |
| 2 |
| c |
| a |
| ||
| 2 |
��
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
��3���ɣ�1������M(
| ||
| 3 |
�����裬��
| 3 |
| ||
| 3 |
| ||
| 3 |
��b=
2
| ||
| 3 |
2
| ||
| 3 |
��ֱ��MF1�ķ���Ϊ
| x | ||||
|
| y |
| c |
��ֱ��DF2�ķ���Ϊ-
| x | ||||
|
| y |
| c |
���ɢ٢ڣ���ֱ��MF1��ֱ��DF2�Ľ���Q(
4
| ||
| 3 |
��֪kOQ=
3
| ||
| 4 |
��ֱ��MF1��ֱ��DF2�Ľ���Q�ڶ�ֱ��y=
3
| ||
| 4 |
���������⿼��Բ���ߵ����ʺ�Ӧ�ã�����ʱҪ�������⣬��ϸ���ע��Բ���ߵ����ʺ�ʽ�ĺ������ã�

��ϰ��ϵ�д�
�����Ŀ
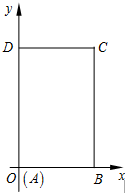 ��ͼ����ƽ��ֱ������ϵxOy�У���֪����ABCD������AB��CD�ֱ�����x�ᡢy����������ϣ���AB=2��AD=4����A������ԭ���غϣ��ֽ������۵���ʹ��A�����߶�DC�ϣ����ۺ����ڵ�ֱ�ߵ�б��Ϊk����д���ۺ�����ֱ�ߵķ��̼�k�ķ�Χ��
��ͼ����ƽ��ֱ������ϵxOy�У���֪����ABCD������AB��CD�ֱ�����x�ᡢy����������ϣ���AB=2��AD=4����A������ԭ���غϣ��ֽ������۵���ʹ��A�����߶�DC�ϣ����ۺ����ڵ�ֱ�ߵ�б��Ϊk����д���ۺ�����ֱ�ߵķ��̼�k�ķ�Χ��