题目内容
若关于x的实系数方程x2+ax+b=0有两个根,一个根在区间(0,1)内,另一根在区间(1,3)内,记点(a,b)对应的区域为S.
(1)设z=2a-b,求z的取值范围;
(2)过点(-5,1)的一束光线,射到x轴被反射后经过区域S,求反射光线所在直线l经过区域S内的整点(即横纵坐标为整数的点)时直线l的方程.
答案:
解析:
解析:
|
解:方程x2+ax+b=0的两根在区间(0,1)和(1,3)上的几何意义是:函数y=f(x)=x2+ax+b与x轴的两个交点的横坐标分别在区间(0,1)和(1,3)内,由此可得不等式组 (1)令z=2a-b,则直线b=2a-z经过点A时Z取得最小值,经过点C时Z取得最大值,即Zmin=-11,Zmax=-2,又A,B,C三点的值没有取到,所以-11<z<-2;8分 (2)过点(-5,1)的光线经x轴反射后的光线必过点(-5,-1),由图可知可能满足条件的整点为(-3,1),(-3,2),(-2,2),(-2,1),再结合不等式知点(-3,1)符合条件,所以此时直线方程为:y+1=
|

练习册系列答案
相关题目
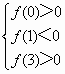 ,即
,即 ,则在坐标平面aOb内,点(a,b)对应的区域S如图阴影部分所示,易得图中A,B,C三点的坐标分别为(-4,3),(-3,0),(-1,0),4分
,则在坐标平面aOb内,点(a,b)对应的区域S如图阴影部分所示,易得图中A,B,C三点的坐标分别为(-4,3),(-3,0),(-1,0),4分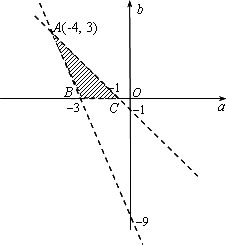
 (2010•黄冈模拟)若关于x的实系数方程x2+ax+b=0有两个根,一个根在区间(0,1)内,另一根在区间(1,3)内,记点(a,b)对应的区域为S.
(2010•黄冈模拟)若关于x的实系数方程x2+ax+b=0有两个根,一个根在区间(0,1)内,另一根在区间(1,3)内,记点(a,b)对应的区域为S. 有两个根,一个根在区间
有两个根,一个根在区间 内,另一根在区间
内,另一根在区间 内,记点
内,记点 对应的区域为S。那么区域S的面积是_______.
对应的区域为S。那么区域S的面积是_______. 有两个根,一个根在区间
有两个根,一个根在区间 内,另一根在区间
内,另一根在区间 内,记点
内,记点 对应的区域为S。那么区域S的面积是_______.
对应的区域为S。那么区域S的面积是_______.