题目内容
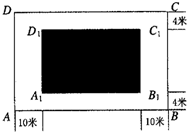 某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲 区A1B1C1D1(阴影部分)和环公园人行道组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米.要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?
某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲 区A1B1C1D1(阴影部分)和环公园人行道组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米.要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?分析:先表示出休闲区的面积,再利用基本不等式求解即可.
解答:解:设A1B1=x,则B1C1=
,…(2分)
∴S=(x+20)(
+8)=4160+8x+
,(x>0)…(6分)
∴S=4160+8x+
≥4160+2
=5760.…(9分)
当且仅当8x=
即x=100时取等号.…(11分)
∴要使公园所占面积最小,休闲区A1B1C1D1的长为100米、宽为40米.…(12分)
| 4000 |
| x |
∴S=(x+20)(
| 4000 |
| x |
| 80000 |
| x |
∴S=4160+8x+
| 80000 |
| x |
8x•
|
当且仅当8x=
| 80000 |
| x |
∴要使公园所占面积最小,休闲区A1B1C1D1的长为100米、宽为40米.…(12分)
点评:本题考查基本不等式的运用,考查利用数学知识解决实际问题,正确表示休闲区的面积是关键.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
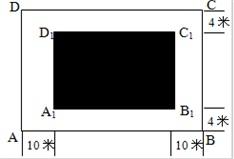 某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1和环公园人行道(阴影部分)组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米(如图)
某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1和环公园人行道(阴影部分)组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米(如图) 某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米.
某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米.
