题目内容
 某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米.
某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米.(1)若设休闲区的长A1B1=x米,求公园ABCD所占面积S关于x的函数S(x)的解析式;
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?
分析:(1)利用休闲区A1B1C1D1的面积为4000平方米,表示出B1C1=
,进而可得公园ABCD所占面积S关于x的函数S(x)的解析式;
(2)利用基本不等式确定公园所占最小面积,即可得到结论.
| 4000 |
| x |
(2)利用基本不等式确定公园所占最小面积,即可得到结论.
解答:解:(1)由A1B1=x米,知B1C1=
米
∴S=(x+20)(
+8)=4160+8x+
(x>0)
(2)S=4160+8x+
≥4160+2
=5760
当且仅当8x=
,即x=100时取等号
∴要使公园所占面积最小,休闲区A1B1C1D1的长为100米、宽为40米.
| 4000 |
| x |
∴S=(x+20)(
| 4000 |
| x |
| 80000 |
| x |
(2)S=4160+8x+
| 80000 |
| x |
8x•
|
当且仅当8x=
| 80000 |
| x |
∴要使公园所占面积最小,休闲区A1B1C1D1的长为100米、宽为40米.
点评:本题考查函数模型的构建,考查基本不等式的运用,注意使用条件:一正二定三相等.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
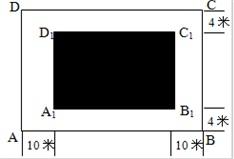 某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1和环公园人行道(阴影部分)组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米(如图)
某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1和环公园人行道(阴影部分)组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米(如图)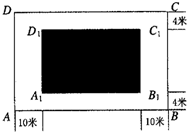 某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲 区A1B1C1D1(阴影部分)和环公园人行道组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米.要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?
某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲 区A1B1C1D1(阴影部分)和环公园人行道组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米.要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?
