题目内容
数列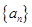 的通项为
的通项为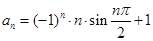 前
前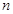 项和为
项和为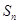 , 则
, 则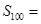 _________.
_________.
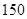
解析试题分析:由数列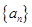 的通项公式得,
的通项公式得, ,四项为一组,每组的和都是6,故
,四项为一组,每组的和都是6,故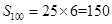 .
.
考点:1、数列的通项公式;2、数列的前n项和.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
题目内容
数列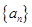 的通项为
的通项为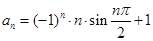 前
前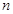 项和为
项和为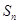 , 则
, 则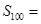 _________.
_________.
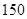
解析试题分析:由数列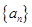 的通项公式得,
的通项公式得, ,四项为一组,每组的和都是6,故
,四项为一组,每组的和都是6,故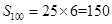 .
.
考点:1、数列的通项公式;2、数列的前n项和.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案