题目内容
 如图,放置的边长为1的正方形PABC沿x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为
如图,放置的边长为1的正方形PABC沿x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为π+1
π+1
.分析:由题意可知,函数的零点以4为周期周期出现,前四分之一周期f(x)的图象为四分之一圆周,后四分之一周期的图象为四分之一圆周,中间半个周期为以
为半径的扇形弧,分别求出面积即可得到答案.
| 2 |
解答:解:如图,

点P(x,y)在运动时,零点以4为周期周期出现,前四分之一周期f(x)的图象为四分之一圆周,后四分之一周期的图象为四分之一圆周,且半径都是1,此时两部分所占面积为
π,中间半个周期为以
为半径的扇形弧,所占面积为
×
×(
)2+1=
+1.
所以y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为
+
+1=π+1.
故答案为π+1.

点P(x,y)在运动时,零点以4为周期周期出现,前四分之一周期f(x)的图象为四分之一圆周,后四分之一周期的图象为四分之一圆周,且半径都是1,此时两部分所占面积为
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| 2 |
| π |
| 2 |
所以y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为
| π |
| 2 |
| π |
| 2 |
故答案为π+1.
点评:本题考查了根据实际问题选择函数模型,考查了数形结合的解题思想方法,解答的关键是正确得到函数f(x)的图象与x所围成的区域,是中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
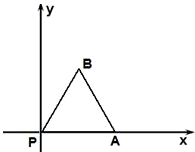 如图,放置的边长为1的正三角形PAB沿 x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系式是y=f(x),记f(x)的最小正周期为T;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积记为S,则S•T=
如图,放置的边长为1的正三角形PAB沿 x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系式是y=f(x),记f(x)的最小正周期为T;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积记为S,则S•T=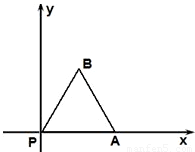 如图,放置的边长为1的正三角形PAB沿 x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系式是y=f(x),记f(x)的最小正周期为T;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积记为S,则S•T= .
如图,放置的边长为1的正三角形PAB沿 x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系式是y=f(x),记f(x)的最小正周期为T;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积记为S,则S•T= .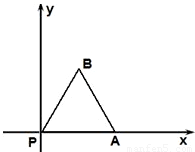 如图,放置的边长为1的正三角形PAB沿 x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系式是y=f(x),记f(x)的最小正周期为T;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积记为S,则S•T= .
如图,放置的边长为1的正三角形PAB沿 x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系式是y=f(x),记f(x)的最小正周期为T;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积记为S,则S•T= .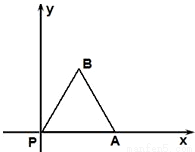 如图,放置的边长为1的正三角形PAB沿 x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系式是y=f(x),记f(x)的最小正周期为T;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积记为S,则S•T= .
如图,放置的边长为1的正三角形PAB沿 x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系式是y=f(x),记f(x)的最小正周期为T;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积记为S,则S•T= .