题目内容
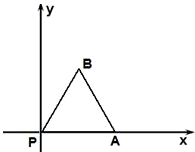 如图,放置的边长为1的正三角形PAB沿 x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系式是y=f(x),记f(x)的最小正周期为T;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积记为S,则S•T=
如图,放置的边长为1的正三角形PAB沿 x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系式是y=f(x),记f(x)的最小正周期为T;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积记为S,则S•T=分析:由已知中长为1的正三角形PAB沿 x轴滚动,我们易画出滚动过程中点P的国轨迹,顶点P(x,y)的纵坐标与横坐标的函数关系式是y=f(x),由图象我们易分析出f(x)的最小正周期T的值,;由其点P的轨迹图象可以得出其轨迹与X轴所围成的图形是一个个相邻的半圆,即两零点之间的图象与X轴围成的图形是2个
圆,由公式计算出面积即可得到答案.
| 1 |
| 3 |
解答:解:由已知中边长为1的正三角形PAB沿 x轴滚动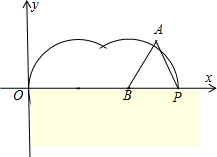
则滚动二次后,P点的纵坐标和起始位置一样第三次滚动时以点P为圆心,故点P不动,
故函数y=f(x)是以3为周期的周期函数,即T=3
两个相邻零点间的图象与x轴所围区域的面积如下图所示:
由图可知,其两个零点之间所围成的面积为以1为半径的2个
圆再加上一个边长为1的正三角形的面积,故其面积是
+
,即S=
+
,
所以S×T=2π+
,
故答案为:2π+

则滚动二次后,P点的纵坐标和起始位置一样第三次滚动时以点P为圆心,故点P不动,
故函数y=f(x)是以3为周期的周期函数,即T=3
两个相邻零点间的图象与x轴所围区域的面积如下图所示:
由图可知,其两个零点之间所围成的面积为以1为半径的2个
| 1 |
| 3 |
| 2π |
| 3 |
| ||
| 4 |
| 2π |
| 3 |
| ||
| 4 |
所以S×T=2π+
3
| ||
| 4 |
故答案为:2π+
3
| ||
| 4 |
点评:本题考查的知识点是函数的图象及图象变化,其中根据已知条件画出满足条件的函数的图象,是解答本题的关键.本题较抽象,其中判断周期易出错,要明白研究的函数是点P的横纵坐标之间的函数的关系,如此则不易出错了

练习册系列答案
相关题目
 如图,放置的边长为1的正方形PABC沿x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为
如图,放置的边长为1的正方形PABC沿x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为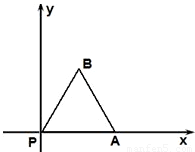 如图,放置的边长为1的正三角形PAB沿 x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系式是y=f(x),记f(x)的最小正周期为T;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积记为S,则S•T= .
如图,放置的边长为1的正三角形PAB沿 x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系式是y=f(x),记f(x)的最小正周期为T;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积记为S,则S•T= .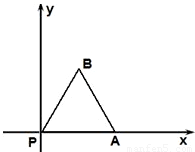 如图,放置的边长为1的正三角形PAB沿 x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系式是y=f(x),记f(x)的最小正周期为T;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积记为S,则S•T= .
如图,放置的边长为1的正三角形PAB沿 x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系式是y=f(x),记f(x)的最小正周期为T;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积记为S,则S•T= .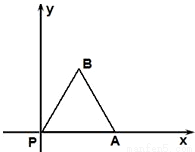 如图,放置的边长为1的正三角形PAB沿 x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系式是y=f(x),记f(x)的最小正周期为T;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积记为S,则S•T= .
如图,放置的边长为1的正三角形PAB沿 x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系式是y=f(x),记f(x)的最小正周期为T;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积记为S,则S•T= .