题目内容
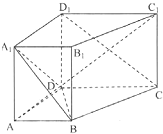 如图,在直四棱柱(侧棱与底面垂直的四棱柱)ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC,给出以下结论:
如图,在直四棱柱(侧棱与底面垂直的四棱柱)ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC,给出以下结论:
(1)异面直线A1B1与CD1所成的角为45°;
(2)D1C⊥AC1;
(3)在棱DC上存在一点E,使D1E∥平面A1BD,这个点为DC的中点;
(4)在棱AA1上不存在点F,使三棱锥F-BCD的体积为直四棱柱体积的 .
.
其中正确的个数有
- A.1
- B.2
- C.3
- D.4
C
分析:直接利用已知条件推出异面直线所成的角判断(1)的正误;通过直线与平面的位置关系判断(2)的正误;通过直线与平面的平行判断(3)的正误;几何体的体积判断(4)的正误即可.
解答: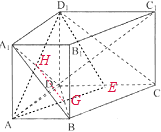 解:(1)由题意可知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC,所以△DD1C1是等腰直角三角形,A1B1∥C1D1,异面直线A1B1与CD1所成的角为45°,所以(1)正确.
解:(1)由题意可知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC,所以△DD1C1是等腰直角三角形,A1B1∥C1D1,异面直线A1B1与CD1所成的角为45°,所以(1)正确.
(2)由题意可知,AD⊥平面DD1C1C,四边形DD1C1C是正方形,所以D1C⊥DC1,
可得D1C⊥AC1;(2)正确;
对于(3)在棱DC上存在一点E,使D1E∥平面A1BD,这个点为DC的中点,因为
DC=DD1=2AD=2AB,如图HG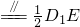 ,所以E为中点,正确.
,所以E为中点,正确.
(4)设AB=1,则棱柱的体积为: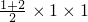 =
= ,当F在A1时,A1-BCD的体积为:
,当F在A1时,A1-BCD的体积为: =
= ,显然体积比为
,显然体积比为
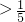 ,所以在棱AA1上存在点F,使三棱锥F-BCD的体积为直四棱柱体积的
,所以在棱AA1上存在点F,使三棱锥F-BCD的体积为直四棱柱体积的 ,所以(4)不正确.
,所以(4)不正确.
正确结果有(1)、(2)、(3).
故选C.
点评:本题考查棱柱的结构特征,几何体的体积的求法,直线与平面的位置关系的判断,考查空间想象能力计算能力.
分析:直接利用已知条件推出异面直线所成的角判断(1)的正误;通过直线与平面的位置关系判断(2)的正误;通过直线与平面的平行判断(3)的正误;几何体的体积判断(4)的正误即可.
解答:
 解:(1)由题意可知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC,所以△DD1C1是等腰直角三角形,A1B1∥C1D1,异面直线A1B1与CD1所成的角为45°,所以(1)正确.
解:(1)由题意可知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC,所以△DD1C1是等腰直角三角形,A1B1∥C1D1,异面直线A1B1与CD1所成的角为45°,所以(1)正确.(2)由题意可知,AD⊥平面DD1C1C,四边形DD1C1C是正方形,所以D1C⊥DC1,
可得D1C⊥AC1;(2)正确;
对于(3)在棱DC上存在一点E,使D1E∥平面A1BD,这个点为DC的中点,因为
DC=DD1=2AD=2AB,如图HG
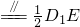 ,所以E为中点,正确.
,所以E为中点,正确.(4)设AB=1,则棱柱的体积为:
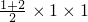 =
= ,当F在A1时,A1-BCD的体积为:
,当F在A1时,A1-BCD的体积为: =
= ,显然体积比为
,显然体积比为
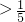 ,所以在棱AA1上存在点F,使三棱锥F-BCD的体积为直四棱柱体积的
,所以在棱AA1上存在点F,使三棱锥F-BCD的体积为直四棱柱体积的 ,所以(4)不正确.
,所以(4)不正确.正确结果有(1)、(2)、(3).
故选C.
点评:本题考查棱柱的结构特征,几何体的体积的求法,直线与平面的位置关系的判断,考查空间想象能力计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
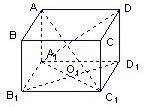 如图,在直四棱柱ABCD-A1B1C1D1中,底面是边长为1的菱形,侧棱长为2.
如图,在直四棱柱ABCD-A1B1C1D1中,底面是边长为1的菱形,侧棱长为2. 如图,在直四棱柱(侧棱与底面垂直的四棱柱)ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC,给出以下结论:
如图,在直四棱柱(侧棱与底面垂直的四棱柱)ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC,给出以下结论: .
.
 如图,在直四棱柱(侧棱与底面垂直)
如图,在直四棱柱(侧棱与底面垂直)